Вычисление определителя и обратной матрицы

Задача вычисления определителя решается методом исключения Гаусс. Т.к. сложение или вычитание строк матрицы коэффициентов не меняет значения определителя, то и сведение исходной матрицы к треугольной не изменяет определитель.

Известно, что определитель треугольной матрицы = произведению ее диагональных коэффициентов.

Знак определителя зависит от того четной или не четной была суммарная перестановка строк матрицы. Таким образом для вычисления определителя надо выполнить прямой ход метода Гаусса для системы уравнений вида AX=0 и найти произведение ведущих коэффициентов.

Рассмотрим алгоритм вычисления обратной матрицы.

Пусть A (матрица коэффициентов) не особенная матрица порядка n.

Обратной к матрице A называют матрицу 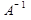для которой справедливо соотношение 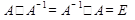. Где Е – единичная матрица, все элементы которой равны 0 кроме диагональных. Нахождением обратной матрицы называют обращением матрицы. И приведенное соотношение лежит в основе алгоритма обращения. Умножая матрицу А на обратную и приравнивая каждый элемент произведения соответствующему элементу единичной матрицы Е получают систему 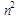уравнений с 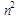неизвестных 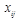— элементами обратной матрицы. При этом коэффициенты при неизвестных – элементы исходной матрицы A, а свободные члены – элементы единичной матрицы E.

Умножим почленно каждую строку матрицы А на 1 столбец обратной матрицы 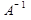и приравняем сумму полученных произведений соответствующему элементу 1-ого столбца единичной матрицы Е.

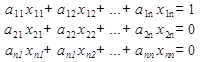
Аналогично при почленном умножении строка матрицы А на 2 столбец обрантной матрицы 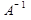получаем еще 1 систему уравнений. И т. д.

Таким образом система из 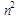уравнений с 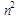неизвестных распадается на n систем уравнений с n неизвестных. Которые имеют 1 и ту же матрицу коэффициентов А и отличаются только столбцом свободных членов. Значит приведение матрицы А к треугольному виду выполняется только 1 раз, а так как в схеме Гаусса основные вычисления связаны с этой исходной матрицей А, то решение всех систем уравнений можно объединить в 1 схеме. Рассматривая одновременно n столбцов свободных членов. Объем вычислений определен примерно 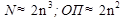. Обычно после определения элементов обратной матрицы рекомендуется проверить вычисления подстановкой в формулу .

Из-за округлений в процессе вычислений могут обнаружится искажения, которые потребуют уточнения элементов приниженной обратной матрицы. Для этого применяют метод итераций.

Обозначим обратную матрицу с приближенным значением элементов с приближенным значением 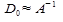. А далее строится

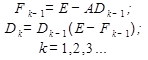
Матрица на каждом шаге 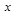характеризует степень близости 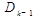к обратной матрице 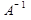. Итерационный процесс продолжают до тех пор пока элементы матрицы 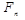по модулю не станут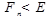

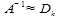
Предлагаемый метод уточнения полезен в совокупности с точными методами, которые приводят к значительным погрешностям из-за большого количества операций и скруглений.

Поиск по сайту: