 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод Гаусса (метод элементарных преобразований)
Рассмотрим две матрицы А и Е (Е – единичная матрица того же порядка, что и А). Преобразуем матрицу А так, чтобы она превратилась в единичную, это эквивалентно ее умножению на обратную матрицу 
. Если те же самые преобразования применить к единичной матрице, то она перейдет в (т.к. 
). Для преобразования матриц А и Е используют перестановку строк местами, умножение или деление всех элементов строки на одно и то же число, не равное 0, прибавление к элементам одной строки соответствующих элементов другой строки (возможно, умноженных на какое-либо число).
Пример 1. Найдем обратную матрицу для матрицы 
.
Запишем рядом с ней единичную матрицу и к элементам второй строки каждой матрицы прибавим элементы первой строки, умноженные на –3; затем к элементам первой строки прибавим элементы второй; на последнем шаге все элементы второй строки разделим на –2:
.
Оставшаяся на месте единичной матрица должна быть обратной к А, проверим это:
.
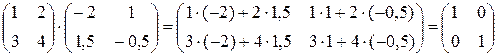Проверка подтверждает, что 
.
Пример 2. Найти обратную матрицу для матрицы 
.
На первом шаге к элементам второй и третьей строки прибавили элементы первой, умноженные на –2; затем разделим вторую строку на –3:
на третьем шаге к элементам первой строки прибавили вторую, умноженную на –2, к третьей – вторую, умноженную на 6; после этого последнюю строчку делим на 9 и прибавляем ее элементы, умноженные на 2, к первой строке, а ко второй строке прибавляем элементы третьей, умноженные на –2:
.
Значит, 
.
Из примеров видно, что при проведении преобразований должна быть определенная последовательность действий: сначала должен быть получен единичный элемент в первой строке и первом столбце, затем нулевые элементы под единицей в первом столбце; затем единица во второй строке и втором столбце, затем нули в этом столбце под единицей и т.д.
Метод Гаусса при своей идейной простоте, может оказаться трудоемким с вычислительной точки зрения, особенно для матриц, элементы которых не являются целыми числами, однако, он может быть очень полезен для одного частного случая, который встречается в экономических задачах.
Поиск по сайту: