АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Способ подстановки

Читайте также:
  1. I. Открытые способы определения поставщика.
  2. II. Решение логических задач табличным способом
  3. III. Глава о необычных способностях.
  4. III. Способы очистки.
  5. Абиотические факторы и приспособления к ним
  6. Абстрактное мышление – высокая способность к обучаемости.
  7. АДАПТАЦИЯ И ОСНОВНЫЕ СПОСОБЫ ПРИСПОСОБЛЕНИЯ ЖИВЫХ ОРГАНИЗМОВ К ЭКСТРЕМАЛЬНЫМ УСЛОВИЯМ СРЕДЫ
  8. Анализ и оценка реальных возможностей восстановления платежеспособности предприятия
  9. Анализ как способ развития экономического мышления
  10. Анализ конкурентоспособности продукции
  11. АНАЛИЗ КРЕДИТОСПОСОБНОСТИ КРЕДИТОПОЛУЧАТЕЛЯ
  12. Анализ ликвидности и платежеспособности

Разберем этот способ на примерах, выбирая для начала самые простые системы из двух линейных уравнений для двух неизвестных – системы .

Пример 1. Решить систему

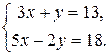
Из первого уравнения выразим через 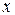, получим . Подставив данное выражение вместо во второе уравнение, получим . Решением этого линейного уравнения является . Используем найденное значение для определения : . Итак, решением системы будет пара чисел: .

Пример 2. Решить систему

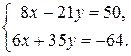
Из второго уравнения выразим 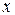через : . Найденное выражение для 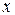подставим в первое уравнение:

.

Умножим обе части последнего уравнения на 3: , откуда найдем , а . Сделав проверку (подставив в оба уравнения системы), убеждаемся, что решением будут .

Второй пример показывает, что решение методом подстановки при своей идейной простоте, требует довольно большого количества вычислений и для систем выше второго порядка практически не применяется.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)