Простейшие действия с матрицами

1) Транспонирование.

Матрица называется транспонированной по отношению к матрице А, если строки одной матрицы являются столбцами другой и наоборот, например,

.

2) Разбиение матриц на блоки.

Разбиением называется выделение в исходной матрице матриц меньшего размера – блоков. Например,

.

Если обозначить выделенные в матрице А блоки:

,

то запись обозначает блочную матрицу А.

3) Сложение (вычитание) матриц.

Чтобы найти сумму или разность двух матриц, нужно сложить или вычесть соответствующие элементы этих матриц, например,

;

.

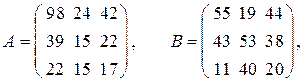
Замечание: исходя из определения, складывать или вычитать можно только матрицы одного размера.

4) Умножение на число (скаляр).

Чтобы умножить матрицу на число, нужно все ее элементы умножить на это число, например,

.

Следствие: общий множитель всех элементов матрицы можно выносить за знак матрицы, разделив при этом все элементы матрицы на выносимый множитель.

Пример. .

Поиск по сайту: