АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Нахождение обратной для матрицы, отличающейся от единичной одним столбцом

Читайте также:
  1. A)нахождение средней из двух соседних средних, для отнесения полученного результата к определенной дате
  2. Автогенератор с емкостной обратной связью
  3. Алг «нахождение минимума»
  4. В 1745 году оброчный сбор стал 55 коп. , в 1760 году поднимается до 1 рубля, в 1768 году до 2-х рублей, в 1785 г.- до 3-х рублей.
  5. Визуализируй лучи света, поднимающиеся вдоль твоего позвоночника
  6. Вывод общей формулы обратной матрицы
  7. Генератор с автотрансформаторной обратной связью
  8. Если рыночная цена в предыдущем примере поднимется до 6 дол., то
  9. Закон Ома для полной цепи с одним Э.Д.С. Последовательное и параллельное соединение потребителей и источников электрической энергии.
  10. Исследование биологической обратной связи.
  11. История Мусы с одним из потомков Израиля и египтянином
  12. Когда поднимается радость, стань ею.

Рассмотрим вначале пару примеров.

.

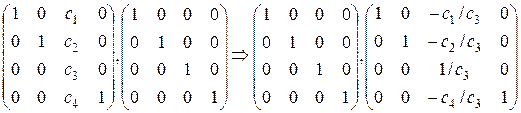Чтобы найти обратную для исходной матрицы, третью строку разделили на 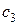, затем к первой строке прибавили третью, умноженную на , ко второй строке – третью, умноженную на , к четвертой – третью, умноженную на .

.

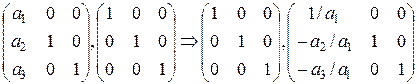Преобразования были следующими: первую строку разделили на 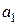, затем ко второй строке добавили первую, умноженную на , а к третьей строке – первую, умноженную на 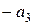. Проанализировав результаты, можем сформулировать правило.

Чтобы найти обратную для матрицы, отличающейся от единичной одним столбцом, нужно единичные столбцы оставить без изменения, а отличающийся столбец преобразовать следующим образом. Элемент на главной диагонали заменить обратным ему, остальные элементы столбца взять с противоположным знаком и разделить на элемент, стоявший на главной диагонали.

Пример. .

2.3. Приближенное нахождение обратной для матрицы вида 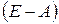, где матрица А такая, что .

Вспомним формулу суммы бесконечно убывающей геометрической прогрессии:

.

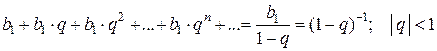Если , формула суммы будет иметь вид:

.

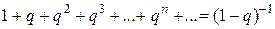По аналогии с данной формулой, заменяя 1 на единичную матрицу Е, а знаменатель прогрессии q на матрицу А, можем написать:

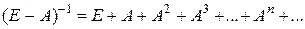
Пример. Возьмем матрицу 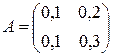, ее норма, равная . Составим Е – А: . Найдем обратную для неё матрицу вначале методом Гаусса.

.

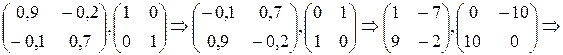
Таким образом .

Теперь найдем обратную матрицу приближенно по формуле:

. Вычислим нужные степени матрицы А:

;

.

.

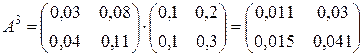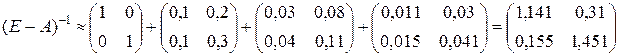Сравнение матриц, найденных двумя способами, показывает их достаточно хорошее совпадение, различия начинаются во втором знаке после запятой. При увеличении числа слагаемых в приближенной формуле точность нахождения обратной матрицы будет увеличиваться.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)