 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Решение систем по формулам Крамера
Формулы Крамера можно получить, используя предыдущий способ решения. Рассмотрим решение системы второго порядка  матричным способом в общем виде:
матричным способом в общем виде:
 .
.
Из полученного равенства следует:
 .
.
Числитель в формуле для  представляет собой определитель вида
представляет собой определитель вида  , вычисленный разложением по первому столбцу. Числитель в формуле для
, вычисленный разложением по первому столбцу. Числитель в формуле для  представляет собой определитель вида
представляет собой определитель вида  , вычисленный разложением по второму столбцу. Тогда можем записать:
, вычисленный разложением по второму столбцу. Тогда можем записать:  , где
, где  – главный определитель системы, составленный из коэффициентов при неизвестных,
– главный определитель системы, составленный из коэффициентов при неизвестных,  – определитель, полученный из главного, заменой коэффициентов при
– определитель, полученный из главного, заменой коэффициентов при  на столбец свободных членов,
на столбец свободных членов, 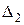 – определитель, полученный из главного, заменой коэффициентов при
– определитель, полученный из главного, заменой коэффициентов при  на столбец свободных членов. Определители
на столбец свободных членов. Определители  и
и 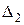 называются вспомогательными.
называются вспомогательными.
Подобные формулы можно получить для любой квадратной системы. Согласно этим формулам:  , где
, где  – главный определитель системы, составленный из коэффициентов при неизвестных,
– главный определитель системы, составленный из коэффициентов при неизвестных,  – определитель, полученный из главного, заменой коэффициентов при
– определитель, полученный из главного, заменой коэффициентов при  на столбец свободных членов.
на столбец свободных членов.
Формулы Крамера являются особенно удобными, когда коэффициенты системы не являются целыми числами.
Пример. Систему линейных уравнений  решить по формулам Крамера.
решить по формулам Крамера.
Вычислим необходимые определители:
 Тогда
Тогда  .
.
Пример. Найти решение системы линейных уравнений

по формулам Крамера.
Выпишем и вычислим главный и все вспомогательные определители:
 ;
;  ;
;
 ;
;  .
.
По формулам Крамера находим неизвестные:

Сделаем проверку:

Поиск по сайту: