Составление и решение балансового уравнения

Балансовое уравнение появляется в линейной модели экономики (модели Леонтьева) и может применяться для анализа и планирования деятельности предприятия, отрасли, а также экономики страны в целом. Рассмотрим суть этой модели на простейшем примере.

Предприятие производит три вида продукции в количестве 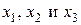единиц каждого вида. Часть этой продукции расходуется внутри производства, а оставшаяся часть (товарная продукция) реализуется за пределами производства, поэтому можно, исходя из условия, что продукция каждого вида должна обеспечивать внутрипроизводственное потребление и запланированный объем продаж, составить систему уравнений:

или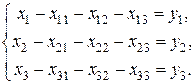

Здесь – количество продукции вида 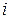, расходуемое на производство продукции вида 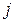, например, 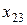– количество продукции второго вида, расходуемое на производство продукции третьего вида. Если разделить это количество на 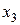, то можно найти, сколько продукции второго вида расходуется при производстве единицы продукции третьего вида. Аналогично, отношение 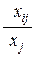– показывает, какое количество продукции вида 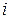расходуется при производстве единицы продукции вида 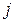. Поскольку такой расход зависит от используемой в производстве технологии, то указанное отношение называется технологическим коэффициентом. 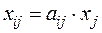Обозначим его и учитывая, что , перепишем вторую систему в виде:

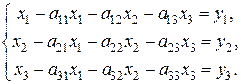
Введем в рассмотрение три матрицы: матрицу А, составленную из технологических коэффициентов (технологическую матрицу или матрицу Леонтьева), матрицу X, характеризующую выпуск продукции (производственный вектор) и матрицу Y (вектор товарной продукции или конечного спроса).

Используя введенные обозначения и помня правила действий с матрицами, систему можно записать в матричном виде:

.

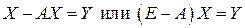Составленное матричное уравнение и называется балансовым уравнением, его решение можно найти с помощью обратной матрицы:

.

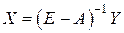Применить его можно следующим способом. По результатам деятельности предприятия за истекший период составляют балансовое уравнение и находят матрицу , которая называется матрицей полных производственных затрат. Элемент этой матрицы 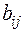равен величине продукции 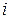-того вида, необходимой для производства единицы товарной продукции 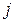-того вида. Затем, зная величину конечного спроса на продукцию 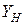на новый производственный период, определим новый производственный вектор 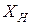по формуле .

Матрицу 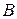можно найти по формуле обратной матрицы через алгебраические дополнения, а можно по приближенной формуле: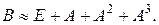

Рассмотрим пример решения задачи с использованием модели Леонтьева.

Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.

Вычислим технологические коэффициенты и составим технологическую матрицу А.

.

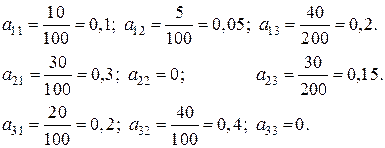
Составим балансовое уравнение 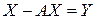и сделаем его проверку.

.

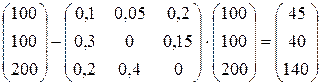Выполним действия в левой части уравнения:

.

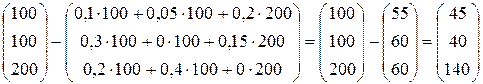Т.к. левая часть уравнения равна правой, значит, уравнение составлено верно.

.

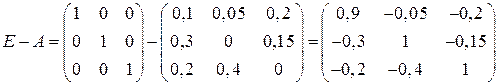Вычислим матрицу полных производственных затрат

а) по формуле обратной матрицы:

.

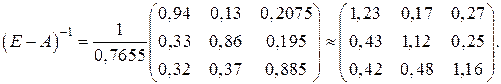
б) по приближенной формуле :

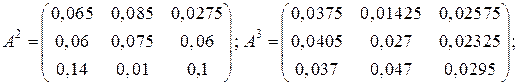
Определим новый производственный план, задав

Поиск по сайту: