Решение систем с помощью обратной матрицы (матричный способ)

Способ основан на том, что любую систему линейных уравнений можно записать в матричном ви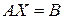де: , где – матрица из коэффициентов при неизвестных, – матрица-столбец из самих неизвестных, 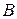– матрица-столбец из свободных членов уравнений.

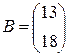Рассмотрим для примера систему . Введем матрицы , , . С помощью этих матриц систему можно записать так: . Выполнив действие в левой части равенства и используя условие равенства матриц, придем снова к исходной системе. В матричном виде можно представить и прямоугольные системы, например, систему 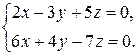можно записать так: .

Итак, всякую систему можно записать в виде матричного уравнения 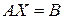. Если матрица в этом уравнении квадратная, то его можно решить по соответствующей формуле: .

Пример. Систему линейных уравнений решить с помощью обратной матрицы.

Выпишем матрицу коэффициентов системы 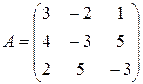и найдем для неё обратную по общей формуле: . Тогда . Таким образом, . Подстановкой найденных значений во все уравнения системы убеждаемся, что оно верное.

Поиск по сайту: