Понятие матрицы, виды матриц

Матрица представляет собой прямоугольный массив чисел, образующих строки и столбцы одинаковой длины.

Отдельные числа, входящие в матрицу, называются ее элементами. Элементы матрицы могут быть любыми действительными и комплексными числами.

Если в матрице m строк и n столбцов, то говорят, что матрица имеет размер 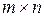. Для краткого обозначения матриц применяются большие латинские буквы A, B, C и т.д. В общем виде элементы матрицы принято обозначать соответствующими малыми латинскими буквами с числами внизу – индексами. Первый индекс указывает номер строки, в которой стоит элемент, второй – номер столбца. Например, 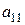– элемент матрицы А, стоящий в первой строке и первом столбце; – элемент матрицы В, стоящий во второй строке и третьем столбце; – элемент матрицы С, стоящий в i -той строке (т.е. в строке с номером i) и j -том столбце (т.е. столбце с номером j). Учитывая введенные обозначения, произвольная матрица А может быть записана так:

.

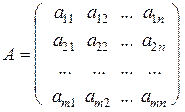Кроме больших круглых скобок, массив чисел, образующих матрицу, может быть заключен в большие квадратные скобки или ограничен сдвоенными чертами. Внутри массива элементы разделяются пробелами. Многоточие в записи означает, что за элементом следуют элементы 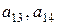и т.д. до ; за элементом следуют элементы 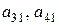и т.д. до элемента 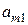. Может применяться и более краткая запись: 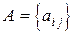, где .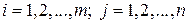

Если в матрице число строк и столбцов совпадает, т.е. , то матрица называется квадратной, а число 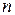указывает порядок матрицы.

Направление из левого верхнего в правый нижний угол квадратной матрицы называется главной диагональю, а элементы 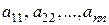— диагональными элементами. Их сумма 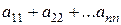, кратко обозначаемая 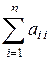, называется следом матрицы 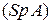. Направление, перпендикулярное главной диагонали, называется побочной диагональю.

Если в квадратной матрице все элементы, стоящие выше или ниже одной из диагоналей, равны 0, например,

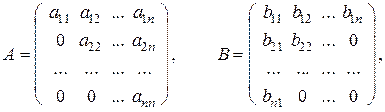
то такие матрицы называются треугольными.

Если равны 0 все элементы, кроме диагональных, то такая матрица называется диагональной:

.

Если все диагональные элементы равны 1, то такая матрица называется единичной:

.

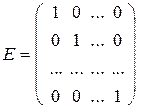Матрица, не обязательно квадратная, все элементы которой равны 0, называется нулевой.

Матрица, состоящая из одного столбца, называется матрицей-столбцом, матрица, состоящая из одной строки, называется матрицей-строкой. Часто оба этих вида матриц называют вектором.

Две матрицы называются равными, если они одного размера и все соответствующие элементы совпадают.

Под нормой матрицы А понимается действительное число , аналогичное понятию модуля для действительных чисел. Из элементов матрицы А ее норму можно составить различными способами, в дальнейшем за норму будем принимать корень квадратный из суммы квадратов всех элементов матрицы:

.

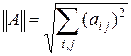Пример. Пусть , тогда

= .

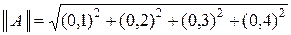Поиск по сайту: