Графический способ решения задачи линейного программирования

К составлению и решению задач линейного программирования приводит необходимость решать различные экономические проблемы. С математической точки зрения линейным программированием называется раздел математики, в котором изучаются методы решения задач на отыскание наибольшего (или наименьшего) значения линейной функции нескольких переменных при наличии ограничений в виде линейных уравнений и неравенств, наложенных на эти переменные.

Графический метод решения подобной задачи рассмотрим на примере.

Пример. Найти наибольшее и наименьшее значения функции 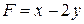при выполнении ограничений: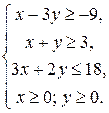

Вначале отметим на координатной плоскости область, в которой выполняются все указанные условия: область допустимых решений (ОДР). Для этого нарисуем границы области, которые задаются следующими линиями: . Линии 4) и 5) совпадают с координатными осями, чтобы нарисовать остальные, отметим по две точки, которые принадлежат этим линиям. Удобно в качестве таковых брать точки, расположенные на координатных осях. Чтобы их найти, приведем уравнения прямых линий к виду уравнений прямой “в отрезках”: 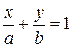. Прямая линия проходит через значения 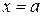и , отложенные на соответствующих осях. Привести уравнения прямых к уравнению “в отрезках” можно разделив обе части уравнения на число, стоящее в правой части:

Каждая прямая делит координатную плоскость на две полуплоскости, в одной из которых выполняется заданное неравенство, а в другой не выполняется. Чтобы определить, с какой стороны от прямой выполняется соответствующее неравенство, подставляем в левую часть неравенства координаты какой-нибудь точки, не лежащей на прямой, например, начало координат. Подставляя эти значения х и у в первое неравенство, получим 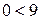. Значит, первое неравенство выполняется ниже прямой 1), т.к. начало координат находится под прямой 1).Отмечаем этот факт штриховкой с соответствующей стороны линии. Аналогичным образом находим полуплоскости, в которых выполняются остальные неравенства. Из рис. 1 видно, что все неравенства вместе выполняются в четырехугольнике ABCD, который и будет областью допустимых решений (ОДР).

Чтобы найти, в какой точке этой области достигается наибольшее значение функции 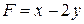, а в какой – наименьшее, нанесем на координатную плоскость линии уровня функции 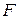. Линиями уровня называются линии, на которых функция принимает постоянное значение. Чтобы их нарисовать, укажем для 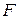какое-либо значение, например, Тогда первая линия уровня задается уравнением 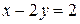. Она проходит через точки (0;-1) и (2;0), изображена пунктиром. Если взять для 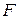значение 4, получим вторую линию уровня 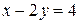, она проходит через точки (0;-2) и (4;0), также изображена пунктиром.

Из рис. 1 видно, что чем больше значение функции, тем ниже проходит линия уровня, и наоборот. Следовательно, наибольшее значение функции 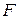достигается в точке С, через которую пройдет самая низко расположенная линия уровня, наименьшее значение достигается в точке А, через которую пройдет наиболее высоко расположенная линия уровня.

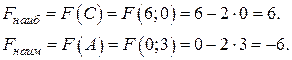
В рассматриваемом примере ОДР замкнута, поэтому в ней можно найти и наибольшее и наименьшее значение произвольной линейной функции. Если ОДР незамкнута, то можно найти или наибольшее или наименьшее значение в зависимости от вида области.

В качестве первого примера была рассмотрена абстрактная математическая задача, однако многие экономические задачи после их формализации также являются задачами линейного программирования. Одна из самых распространенных задач такого рода – задача оптимального использования ресурсов. Рассмотрим её в одном из простейших вариантов.

Для изготовления различных изделий А и В предприятие использует три вида сырья На производство единицы изделия А требуется затратить сырья первого вида 6 кг, сырья второго вида 5 кг, третьего – 3 кг. На производство единицы изделия В соответственно 3, 10 и 12 кг. Производство обеспечено сырьем первого вида в количестве 714 кт, сырьем второго вида в количестве 910 кг и сырьем третьего вида – 948 кг. Прибыль от реализации единицы готового изделия А составляет 3 тыс. руб., изделия В - 9 тыс. руб. Составить план производства изделий А и В, при котором прибыль от их реализации максимальна.

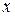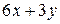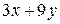Формализуем условие этой задачи. Пусть – планируемое количество изделий А, – планируемое количество изделий В, тогда затраты сырья первого вида на их производство составят кт, сырья второго вида кг, сырья третьего вида кг, прибыль составит тыс. руб.

Учитывая ограничения по количеству сырья и естественное требование, что 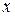и неотрицательны, поставленную задачу можно записать так. Найти наибольшее значение функции прибыли 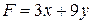при выполнении следующих условий:

Нанесем на чертеж область допустимых решений этой задачи. Вначале рисуем прямые, задаваемые уравнениями:

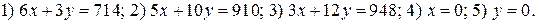
Прямые 1), 2) и 3) предварительно приведем к виду уравнений “в отрезках”.

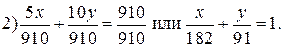
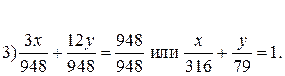
Затем отмечаем те полуплоскости, в которых выполняются заданные неравенства. Все вместе они выполняются в области ОABCD, заштрихованной на рис.2.

Затем отмечаем линии уровня целевой функции, взяв для F два значения: 180 и 360. Линии уровня задаются уравнениями:

Из рис. 2. видно, чем больше значение функции F, тем выше расположена линия. Значит, наибольшее значение F достигается в точке С, через которую пройдет наиболее высоко расположенная линия уровня.

Точка С лежит на пересечении прямых 2) и 3), поэтому для определения ее координат решаем систему:

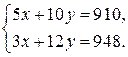
Решение системы дает и 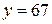. Следовательно, при планируемом производстве 48 единиц изделий А и 67 единиц изделий В прибыль от их реализации будет максимальной и составит (тыс. руб.).

Поиск по сайту: