АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Основные свойства определённого интеграла

Читайте также:
  1. B. Основные принципы исследования истории этических учений
  2. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  3. I.3. Основные этапы исторического развития римского права
  4. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  5. II. Основные задачи и функции
  6. II. Основные показатели деятельности лечебно-профилактических учреждений
  7. II. Основные проблемы, вызовы и риски. SWOT-анализ Республики Карелия
  8. III. Психические свойства личности – типичные для данного человека особенности его психики, особенности реализации его психических процессов.
  9. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  10. SCАDA-системы: основные блоки. Архивирование в SCADA-системах. Архитектура системы архивирования.
  11. VI.3. Наследственное право: основные институты
  12. А) возникновение и основные черты

При перестановке пределов интегрирования знак интеграла меняется на противоположный:

Отрезок интегрирования можно разнообразить на части:

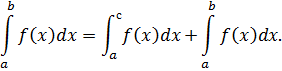
Постоянный множитель можно выносить за знак определенного интеграла:

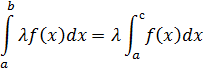
Определённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций:

.

Геометрический смысл определённого интеграла

Определенный интеграл равен площади криволинейной трапеции, образованной графиком функции f(x), осью Ox и прямыми x=a и x=b. .

 

y B y=f(x)

A

 
 

 


S

 
 


0 a b x

 


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)