Применение определённого интеграла к решению физических задач

Определённый интеграл применяется при решении задач на вычисление: работы переменной силы; работы, затраченной на растяжке или сжатие пружины; пути, пройденного телом за промежуток времени; давления жидкости на вертикальную поверхность.

Путь, пройденный телом при равномерном движении со скоростью v=f(t) за промежуток времени [t₁;t₂], вычисляется по формуле

S= .

Согласно закону Гука сила F(x), растягивающая (сжимающая) пружину на x m, пропорциональна этому растяжению (сжатию), т.е. F(x)=kx, где

k - коэффициент пропорциональности. Работа A, совершаемая переменной силой F(x) на отрезке [a;b], вычисляется по формуле

A=

Сила давления p жидкости на вертикальную пластинку, погружённую в жидкость, вычисляется по формуле

p=pg

где g=9,81 м/с²- ускорение свободного падения;

p - плотность жидкости кг/м³;

a,b – изменение глубины погружения пластинки, м.

Вычислить следующие определенные интегралы:

1)

Решение. Находим

2)

Решение. Имеем

3)

Решение. Имеем

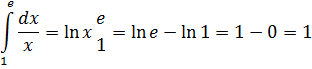
4)

Решение. Имеем

5)

Решение: Имеем

6)

Решение: Имеем

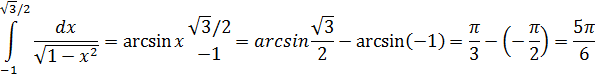
7)

Решение: Имеем

8)

Решение: Введем новую переменную интегрирования с помощью подста-
новки

2х — 1= и. Дифференцируя, имеем 2dx=dи, откуда dx=(1/2) du. Находим-
новые пределы интегрирования. Подставляя в соотношение 2х-1=и
значения х=2 и х=3, соответственно получим =2* 2 — 1=3, =2*3 — 1=5.
Следовательно,

9)

Решение: Положим 5х — 1=и; тогда 5dx=du, dx=(1/5)du. Вычисляем новые пределы интегрирования: =5* 1 — 1=4, =5* 2 — 1=9. Следовательно,

10)

Решение: Положим 2 +1 = и; тогда 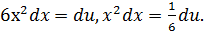. Вычисляем новые пределы интегрирования: . Таким образом,

11)

Решение: Преобразуем подкоренное выражение: . Поло-
жим Зх/2=и, откуда dх=(2/3)du. Найдем новые пределы-интегрирования:
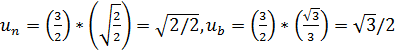. Таким образом:

12)

Решение:

Положим u=ln х, dv=x dx; тогда . Следовательно,

.

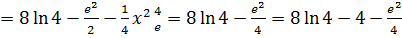Пример: Вычислить площадь фигуры, ограниченной указанными линиями:

x+2у-4=0, у=0, х=-3 и х=2.

Решение:

Выполним построение фигуры. Строим прямую х+2у-4=0 по двум точкам А(4;0) и В(0;2).

Выразив у через х, получим у=- 0,5х+2.

По формуле (1), где ƒ(х)= - 0,5х+2, а=-3, b=2, находим

S= =11,25 (кв.ед.)

В качестве проверки вычислим площадь трапеции М₁ МNN₁ обычным путем. Находим: M₁ M=ƒ(-3)= - 0,5(-3)+2=3,5, N₁ N=ƒ(2)= - 0,5∙2+2=1, М₁ N₁=5. Следовательно, S=0,5(3,5+1)∙5=11,25 (кв.ед.).

Пример: Вычислить площадь фигуры, ограниченной указанными линиями:

у= и у=2х.

Решение: Данная фигура ограничена параболой у = и прямой у = 2х.

Для определения точек пересечения заданных линий решим систему уравнений

откуда находим -2х=0 Используя для нахождения искомой площади формулу (5), получим

S= = (кв.ед.).

Пример: Скорость движения точки изменяется по закону υ=(3t²+2t+1) . Найти путь, пройденный точкой за 10 с от начала движения.

Решение:

Согласно условию, ƒ(t)= 3t²+2t+1, t₁=0, t₂=10. По формуле (6) находим

S= 3t²+2t+1)dt= =10³+10²+10=1110 (м).

Пример: Тело брошено с поверхности земли вертикально вверх со скоростью

υ =(39,2-9,8t) . Найти наибольшую высоту подъема тела.

Решение:

Тело достигнет наибольшей высоты подъема в такой момент времени t, когда υ=0, т. е. 39,2-9,8t=0, откуда t=4 с. По формуле (6) находим

S= 39,2-9,8t)dt= =78,4 (м).

Пример: Сжатие х винтовой пружины пропорционально приложенной силе F. Вычислить работу силы F при сжатии пружины на 0,04 м, если для сжатия ее на 0,01 м нужна сила 10 Н.

Решение:

Так как х=0,01 м при F=10 Н, то, подставляя эти значения в равенство (8), получим 10=k∙0,01, откуда k=1000 . Подставив теперь в это же равенство значение k, находим F=1000 х, т. е. ƒ(х)=1000 х. Искомую работу найдем по формуле (7), полагая a=0, b=0,04:

A= 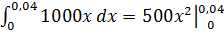=0,8 (Дж).

Пример: Цилиндрическая цистерна с радиусом основания 0,5 м и высотой 2 м заполнена водой. Вычислить работу, которую необходимо произвести, чтобы выкачать воду из цистерны.

Решение: Выделим на глубине х горизонтальный слой высотой dx. Работа А, которую надо произвести, чтобы поднять слой воды весом P на высоту х, равна Px.

Изменение глубины х на малую величину dx вызовет изменение объема V на величину dV= 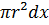и изменение веса P на величину dP=9807 ; при этом совершаемая работа А изменится на величину dA=9807 .

Проинтегрировав это равенство при изменении х от 0 до Н, получим

A= 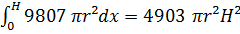=4903 (Дж).

Пример: Треугольная пластинка с основание 0,2 м и высотой 0,4 м погружена вертикально в воду так, что вершина лежит на поверхности воды, а основание параллельно ей. Вычислить силу давления воды на пластинку.

Решение:

Выделим на глубине х горизонтальную полоску шириной dx.

Изменение глубины х на малую величину dx вызовет изменение силы давления Р на малую величину dP. Площадь полоски DEC имеем у:0,2=х:0,4, откуда у=0,5х.

Следовательно,

dP=9,807

Интегрируя dP при изменении х от 0 до 0,4, получим

P=4903,5 =4903,5 =1634,5∙0,4³

Вопросы для закрепления теоретического материала к практической работе.

1. Формула Ньютона-Лейбница.

2. Геометрический смысл определённого интеграла.

3. По какой формуле находится объём тела вращения?

4. Формулы приближенного вычисления определённого интеграла.

1. При решении физических задач какого типа применяются определённый интеграл

Поиск по сайту: