Момент импульса микрочастицы

В классической механике, как мы видели, момент импульса тела выражается формулой:

(II.25)

Его значение определяется тем, что эта величина является интегралом движения в поле центральных сил.

В квантовой механике векторы в формуле (II.25) заменяются соответствующими операторами. И оператор момента импульса записывается так:

(II.26)

является также интегралом движения в поле центральных сил и обладает свойствами аналогичными свойствам момента импульса в классической механике. Он зависит от операторов координат и импульсов следующим образом:

→ (II.27)

Раскрывая определитель (II.27), получим следующее выражение для оператора момента импульса:

(II.28)

В более подробной форме компоненты проекций оператора момента импульса выражаются через компоненты проекций оператора импульса микрочастицы по формулам:

(II.29)

Из формул (II.28) и (II.29) вытекает известное соотношение для квадрата оператора момента импульса, связывающее его с компонентами проекций оператора момента импульса на координатные оси:

(II.30)

Найдем правила перестановки для компонент момента импульса. Для этого вычислим, например, такой коммутатор:

(II.31)

Воспользовавшись формулами (II.29), перепишем данный коммутатор в развернутом виде:

(II.32)

Теперь, вычитая второе равенство из первого, получим значение данного коммутатора.

(II.33)

Аналогично получаются коммутационные соотношения для остальных компонент оператора момента импульса:

(II.34)

Теперь еще раз выпишем окончательный результат для данных коммутационных соотношений:

(II.35)

Таким образом, операторы проекций момента импульса между собой не коммутируют. Если определена одна проекция момента импульса, то две другие не определены. Можно получить путем аналогичных вычислений, что:

(II.36)

То есть, можно выбрать и один из операторов компоненты углового момента, которые взаимно коммутируют, например . При этом обе величины и в принципе могут быть измерены одновременно.

Можно также показать с использованием полиномов Лежандра, что собственные значения оператора квадрата момента импульса будут выражаться формулой:

(II.37)

Соответствующие собственные значения оператора будут:

(II.38)

всего будет 2l+1 значений m_l.

Физический смысл квантовых чисел n, l, m_l заключаются в том, что главное квантовое число n характеризует величину энергии E_n, орбитальное квантовое число l – величину квадрата момента импульса M²_l и магнитное квантовое число m – величину проекции момента импульса M_z на произвольно выделенное направление Oz. Отсюда следует, что возможные значения абсолютной величины момента импульса и возможные значения проекций момента импульса на произвольную ось имеют квантованные значения. Никаких других значений этих величин, кроме приведенных выше, не может быть.

При этом каждое из возможных значений M_x, M_y и M_z, не наделено какими-то особыми свойствами, то есть они абсолютно равноправны. Это вытекает из того, что ни одно из направлений Oz, Ox или Oy не обладает какими-то уникальными преимуществами по сравнению с двумя другими направлениями. Физический смысл этого заключается в том, что, если измерять, например, М_x, то мы получим одно из значений с определенным значением М_x. Это состояние будет состоянием с неопределенными М_y и M_z. Это означает, что измерение одной компоненты импульса дает неопределенное значение двух других. Иными словами одновременное измерение различных компонент импульса взаимно исключается.

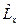Отметим, что для систем со сферической симметрией, например атомов, момент импульса является интегралом движения. То есть это интеграл движения в поле центральных сил. Обычно момент импульса в квантовой механике называется орбитальным моментом и обозначается буквой , а его компоненты - буквами , и .

Поиск по сайту: