АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Эрмитовость операторов

Читайте также:
  1. Взаимная ортогональность собственных функций эрмитовых операторов
  2. Кодирование операторов GPSS/PC
  3. Обработка операторов DML посредством DBMS_SQL
  4. Перегрузка операций. Понятие перегрузки операторов. Синтаксис перегрузки операции. Перегрузка бинарных операций, операций сравнения.
  5. Перечень мер для операторов, являющихся государственными или муниципальными органами
  6. Расчет количества рабочих мест операторов РМТС
  7. Сайты туроператоров

Как мы уже говорили, среднее значение величины 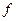равно . В то же время средние значения наблюдаемой физической величины вещественны (действительны, а не комплексны). То есть среднее значение , будучи вещественным (действительным), равно комплексно сопряженному значению , что означает

 

(II.9)

 

Это частный случай следующего выражения

 

(II.10)

Операторы, удовлетворяющие равенствам (II.9) и (II.10), называются эрмитовыми. Заметим, что по определению, если для 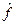имеем , то для ,будет справедливо .

Таким образом, операторы, соответствующие в математическом аппарате квантовой механики вещественным (действительным) физическим величинам, должны быть эрмитовыми.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)