Одноэлектронное приближение, уравнения Хартри

Запишем гамильтониан системы электронов и ядер – то есть атома, молекулы (i, j – номера электронов, a, b – номера ядер):

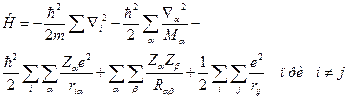(III.21)

здесь первый член – это оператор кинетической энергии электронов, второй член – оператор кинетической энергии ядер, третий член – оператор потенциальной энергии взаимодействия ядер и электронов между собой, четвертый член – оператор потенциальной энергии взаимодействия ядер между собой, пятый член – оператор потенциальной энергии взаимодействия электронов между собой. В силу приближения Борна-Оппенгеймера, оператор кинетической энергии ядер равен нулю. Оператор потенциальной энергии взаимодействия ядер между собой также равен нулю, поскольку его вклад в полную электронную волновую функцию при фиксированных положениях ядер в пространстве постоянен и не зависит от состояния системы.

Тогда гамильтониан может быть записан следующим образом:

, (III.22)

при i≠j

Введем единицы Хартри:

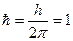
1 а.е. = 0,529177 Å

Тогда:

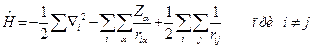(III.23)

и

(III.24)

Запишем формулы, выражающие основные положения одноэлектронного приближения:

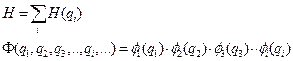(III.25)

причем 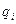– набор пространственных координат частиц – электронов. Можно сказать, что одноэлектронное приближение заключается в двух основных положениях: Гамильтониан системы равен сумме одноэлектронных гамильтонианов, а ее волновая функция равна произведению одноэлектронных волновых функций.

Причем каждый одноэлектронный гамильтониан действует только на одноэлектронную функцию того же самого электрона:

(III.26)

Посмотрим, как связана 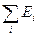в (III.26) с полной энергией системы 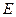. Запишем стационарное уравнение Шредингера в одноэлектронном приближении с учетом того, что здесь одноэлектронные орбитали не содержат спиновых переменных.

(III.27)

С учетом (III.25) получим:

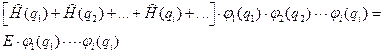
(III.28)

Сумма одноэлектронных гамильтонианов действует на произведение одноэлектронных функций следующим образом: как сказано выше, гамильтониан действует только на волновую функцию 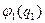, а произведение остальных одноэлектронных волновых функций выносится за знак этого гамильтониана . Аналогичная ситуация имеет место с гамильтонианом 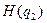и так далее. В результате получается:

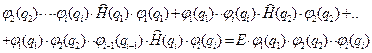(III.29)

Поделим обе части (III.29) на произведение одноэлектронных функций и получим после сокращения в каждом слагаемом волновых функций знаменателя и волновых функций числителя, стоящих перед гамильтонианом:

(III.30)

Далее, учитывая (III.26), получаем:

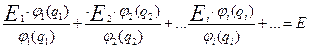(III.30а)

Поскольку 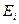не являются операторами, сокращая в каждом слагаемом, имеем:

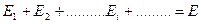(III.31)

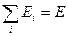(III.32)

Таким образом, получено важное утверждение: В одноэлектронном приближении энергия 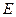всей системы равна сумме одноэлектронных энергий .

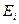Поскольку электроны физически неразличимы, мы имеем фактически всего одно уравнение, которое имеет множество решений. Запишем его для i -го электрона:

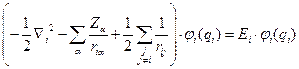(III.33)

Иначе говоря, мы имеем фактически уравнение движения одного электрона в поле других электронов и ядер. Это проясняет физический смысл одноэлектронного приближения. Однако, для практического получения точных решений для различных атомов и молекул необходимо дальнейшее уточнение стационарного уравнения Шредингера.

Необходимо в одноэлектронном приближении ввести эффективный гамильтониан, который содержит вместо члена – член 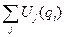. Это связано с тем, что мы не знаем расстояния между движущимися электронами в атоме или молекуле. Физически такая замена соответствует тому, что каждый электрон движется в усредненном поле всех остальных электронов и ядер. Посмотрим, чему равен член 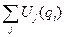, отвечающий потенциальной энергии взаимодействия электронов. Как известно, 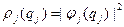– это плотность вероятности обнаружить j-й электрон в единице объема конфигурационного пространства. Если ее умножить на элемент объема конфигурационного пространства 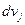, то получим вероятность обнаружить этот j- й электрон в элементе объема 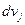. Поле, создаваемое j - м электроном, находящимся в элементе объема 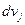, и действующее на i-й электрон в точке с координатами :

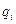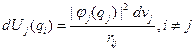.А поле в этой точке, создаваемое j - м электроном, находящимся во всем доступном ему пространстве, - . И, наконец, поле создаваемое всеми электронами, кроме i - го в этой точке пространства определяется выражением:

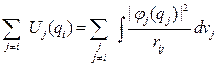(III.34)

Теперь можно сказать, что вместо у нас имеется :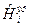

(III.35)

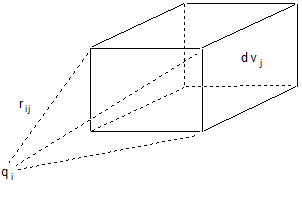
Рис. 10. Точка с координатами q_i и элемент объема конфигурационного пространства dv_{j .}

Стационарное уравнение Шредингера для гамильтониана (III.35) запишется так:

(III.36)

Или более подробно:

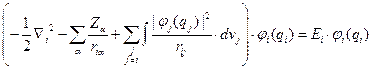(III.37)

i = 1, 2, 3,… (III.38)

Выражение (III.38) представляет собой знаменитые уравнения Хартри (1928 г.). Эти уравнения решаются методом последовательных приближений, то есть методом итераций.

допустим, что мы знаем 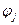, то есть их явный вид. Обозначим их как . Подставим эти одноэлектронные функции в систему уравнений (III.38), а точнее в выражение для потенциала. После чего гамильтониан системы считается известным и систему уравнений (III.38) можно решить. После решения этой системы уравнений получаем набор функций 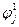, которые затем снова подставляем в выражение для потенциала в уравнениях (III.38). Опять решаем полученные уравнения и так далее, проводя ту же операцию определенное количество раз, добиваемся того, что k –ое и (k + 1)- ое решения будут отличаться не более, чем на заданную величину (точность) , то есть 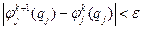. Полученные решения называются самосогласованными.

Необходимо отметить, что даже самосогласованные функции не могут быть точными решениями стационарного уравнения Шредингера для многоэлектронных систем 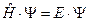, так как здесь истинный гамильтониан заменен эффективным гамильтонианом.

Поиск по сайту: