Средняя энергия системы в одноэлектронном приближении

Как мы только что видели, волновая функция в одноэлектронном приближении для системы, содержащей N электронов, имеет вид:

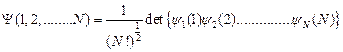(III.46)

Запишем гамильтониан такой системы в виде суммы одно- и двухэлектронной частей:

(III.47)

Тогда средняя энергия системы будет равна:

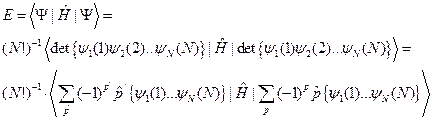(III.48)

Так как 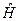действует на все электроны одинаково, то интегралы с одинаковыми перестановками справа и слева от гамильтониана равны между собой и их количество равно 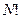.Это интегралы вида

1. одноэлектронные интегралы:

а) без перестановок

б) с одной перестановкой или большим числом перестановок интегралы обращаются в нуль вследствие ортогональности разных функций.

2. двухэлектронные интегралы:

а) без перестановок двух электронов (точнее, функций)

– такие интегралы называются кулоновскими интегралами. Это легко понять, использую аналогию с обычной электростатикой, потому, что под знаком интеграла стоит произведение электронных плотностей (зарядов) двух электронов, деленное на расстояние между ними. Здесь и далее использованы для удобства условные номера электронов (1 и 2).

Суммирование всех таких интегралов дает:

(III.49)

б) с одной перестановкой получается интеграл, не имеющий, в отличие от кулоновского интеграла, классического аналога:

– это обменный интеграл. В нем два электрона распределены по двум одноэлектронным функциям (орбиталям).

Суммирование всех таких интегралов дает выражение:

(III.50)

Все остальные интегралы равны нулю вследствие ортогональности волновых функций. С учетом ортонормированности волновых функций, суммируя одноэлектронные, кулоновские и обменные интегралы, получим выражение для средней энергии системы в одноэлектронном приближении:

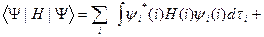
(III.51)

Введено условие , так как в противном случае двухэлектронные интегралы взаимно уничтожаются.

Поиск по сайту: