Импульс

Следующий закон сохранения связан с однородностью пространства, которая означает, что механические свойства замкнутой системы не меняются при параллельном переносе системы как целого в пространстве. При таком переносе системы все ее точки смещаются на один и тот же вектор , т.е. и можно обозначить, что . Так как свойства системы не меняются, то L должна быть постоянной при этом:

(I.15)

Так как вектор произволен, то должно быть:

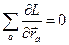(I.16)

И поскольку из уравнений Лагранжа следует, что , то (I.16) можно переписать так: (I.17)

Таким образом, в замкнутой механической системе векторная величина при движении.

– называется импульсом системы.

Дифференцируя функцию Лагранжа, найдем, что

(I.18)

Аддитивность импульса очевидна, поскольку он равен сумме импульсов отдельных частиц, причем независимо от наличия или отсутствия взаимодействия между ними. В обобщенных координатах - обобщенный импульс.

Поиск по сайту: