 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Законы сохранения
Прежде чем говорить о законах сохранения, вспомним о принципе относительности Галилея и о связанном с этим принципом понятии о системах отсчета.
Как известно, для изучения механических явлений надо выбрать ту или иную систему отсчета. Возникает задача отыскания такой системы отсчета, в которой законы механики выглядят наиболее просто.
Оказывается, что всегда можно найти такую систему отсчета, по отношению к которой пространство является однородным и изотропным, а время – однородным. Такая система называется инерциальной. В ней, в частности, свободное тело, покоящееся в некоторый момент времени, остается в покое неограниченно долго. Опыт показывает, что существует бесконечное множество инерциальных систем отсчета, движущихся друг относительно друга равномерно и прямолинейно.
Важнейший принцип механики – принцип относительности Галилея – утверждает, что во всех этих системах свойства пространства и времени одинаковы и одинаковы все законы механики.
Преобразования Галилея отражают этот принцип:
 (I.10)
(I.10)
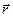 и
и  - координаты одной и той же точки в двух системах отсчета, движущихся друг относительно друга со скоростью
- координаты одной и той же точки в двух системах отсчета, движущихся друг относительно друга со скоростью  . Второе соотношение отражает предположение об абсолютности времени, лежащее в основе классической механики.
. Второе соотношение отражает предположение об абсолютности времени, лежащее в основе классической механики.
При движении механической системы 2s величин 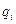 и
и  (i=1,2,…s), определяющих ее состояние, изменяются со временем. Существуют, однако, такие функции этих величин, которые сохраняют при движении свои значения, зависящие только от начальных условий. Эти функции называют интегралами движения.
(i=1,2,…s), определяющих ее состояние, изменяются со временем. Существуют, однако, такие функции этих величин, которые сохраняют при движении свои значения, зависящие только от начальных условий. Эти функции называют интегралами движения.
Число независимых интегралов движения для замкнутой механической системы с s степенями свободы равно 2s - 1. Наиболее важную роль играют энергия (Е), импульс ( ) и момент импульса (
) и момент импульса ( ). Их семь:
). Их семь:

Эти величины обладают свойством аддитивности, означающим, что их значения для систем, состоящих из невзаимодействующих частей (подсистем), равны сумме значений для каждой части в отдельности.
Законы сохранения имеют глубокое происхождение, связанное с фундаментальными свойствами пространства и времени. Роль законов сохранения возросла, когда выяснили, что они выходят за рамки механики и представляют собой универсальные законы природы.
Поиск по сайту: