 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Момент импульса. Рис.1. Вектор бесконечно малого поворота и изменение вектора
Рис.1. Вектор 
бесконечно малого поворота и изменение вектора 
.
Сохранение момента импульса связано с изотропией пространства, которая означает сохранение механических свойств замкнутой системы при любом повороте ее как целого в пространстве. Поскольку при таком повороте не меняются свойства системы, то не должна меняться и функция Лагранжа, описывающая эти свойства. Рассмотрим бесконечно малый поворот системы и положим, что ее функция Лагранжа при этом не изменяется. Введем вектор бесконечно малого поворота, абсолютная величина которого равна углу 
, а направление совпадает с осью поворота (Рис.1.). Найдем изменение вектора , проведенного из начала координат в произвольную точку поворачиваемой системы. 
Линейное перемещение конца радиус–вектора связано с углом соотношением:
(I.21)
Поскольку направление поворота перпендикулярно плоскости, проходящей через и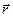 
, ясно, что
(I.22)
Так как при повороте системы меняется направление всех ее векторов, то
(I.23)
Условия постоянства L при повороте означает что:
(I.24)
Заменяем в (I.24) 
и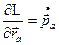 
. Получаем с учетом (I.22) и (I.23):
(I.25)
мы вынесли за знак суммы потому, что он одинаков для всех точек системы и поэтому не зависит от номера частицы a. Ввиду произвольности , отсюда следует, что:
(I.26)
но это выражение равно:
(I.27)
Это означает, что величина под знаком производной не зависит от времени:
(I.28)
Эта величина называется моментом импульса механической системы. Ее аддитивность очевидна, причем, как и у импульса, она не зависит от наличия или отсутствия взаимодействия между частицами.
Этим исчерпываются аддитивные интегралы движения. Таким образом, всякая замкнутая система имеет всего семь таких интегралов: энергия по три компоненты векторов импульса и момента импульса:
Е, Px, Py, Pz, Mx, My, Mz
Можно показать, что кинетическая энергия системы двух материальных точек равна:
(I.29)
Здесь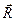 
– радиус-вектор, проведенный из начала координат в центр масс этой системы, 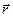– вектор, проведенный из одной точки в другую, а 
– приведенная масса.
Если поместить начало отсчета в центр масс, то 
и 
. Такой подход очень полезен, например, при рассмотрении вращения двухатомной молекулы.
Поиск по сайту: