Свободная частица

Свободная частица движется в поле с постоянным потенциалом, т.е. имеет постоянную потенциальную энергию, которую можно положить равной нулю (U = 0). Тогда стационарное уравнение Шредингера будет таким:

(II.74)

(II.74) – дифференциальное уравнение второго порядка с постоянными коэффициентами, поэтому его решения можно искать в виде:

(II.75)

(II.76)

Можно считать, что в состоянии частица движется в положительном направлении оси Oх с импульсом . В состоянии - в противоположном направлении. Пусть, например частица находится в состоянии, описываемом волновой функцией . Какие отсюда вытекают физические следствия? E не может быть < 0, так как при E < 0 (точнее E < U) экспоненциальный множитель становится действительным числом и при , . То есть волновая функция в этом случае утрачивает физический смысл. Рассмотрим квадрат модуля волновой функции, который на основании (II.75) и (II.76) равен . Следовательно, вероятность нахождения частицы не зависит от положения частицы вдоль оси О х, и вероятность ее нахождения в любом месте одномерного пространства, где она совершает движение, одинакова. Перепишем (II.75) в виде:

, (II.77)

где k – волновой вектор, так как в многомерном пространстве он действительно является векторной величиной. Из (II.77) имеем:

(II.78)

Вспомнив формулу, связывающую длину волны де Бройля с импульсом частицы, получаем:

→

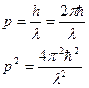→ (II.79)

Таким образом, при свободном движении у частицы строго определен импульс, но неопределенность её положения бесконечно велика.

Поиск по сайту: