Туннельный эффект. Если есть две области пространства, в которых потенциальная энергия частицы меньше, чем на поверхности

Если есть две области пространства, в которых потенциальная энергия частицы меньше, чем на поверхности, разделяющей эти области, то говорят, что эти области разделены потенциальным барьером. В классической механике потенциальный барьер непроницаем для частиц, энергия которых меньше величины барьера. В квантовой механике это не так.

Явление прохождения частицы с отличной от нуля вероятностью сквозь потенциальный барьер называется туннельным эффектом. На Рис.2 изображен потенциальный барьер в одном измерении, соответствующем движению частицы вдоль оси х.

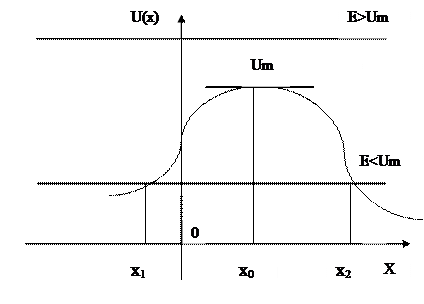
Рис. 2. Схематическое изображение потенциального барьера при движении частицы вдоль оси Х.

Здесь U(x) – потенциальная энергия, которая максимальна в точке х₀. Все пространство в этой точке делится на две област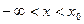и и 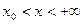, в которых .

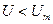Значение термина потенциальный барьер (ПБ) прояснится, если мы рассмотрим движение частицы в поле 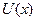на основе классической механики. Полная энергия частицы равна:

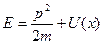
Отсюда импульс частицы равен:

.

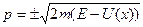Если Е больше высоты потенциального барьера U_m, то выражение под корнем положительно и частица свободно пройдет барьер слева направо, если р > 0 и справа налево, если р < 0.

Пусть, например, частица движется слева, имея полную энергию Е, меньшую, чем U_m. Тогда в некоторой точке x₁ E = U(x) и p(x₁) = 0 частица остановится. Вся её энергия превратится в потенциальную энергию, и она будет двигаться в обратном направлении. Поэтому, если E < U_m, то частица не пройдет сквозь барьер.

Таким образом, в классической механике потенциальный барьер полностью непрозрачен для частиц с E < U_m и полностью прозрачен для частиц с E > U_m. Этим и объясняется название ПБ.

Совсем иначе обстоит дело вблизи барьеров, если речь идет о движении микроскопических частиц, то есть о движении, при рассмотрении которого нельзя пренебрегать квантовыми эффектами. В этом случае, как мы сейчас увидим, частицы с энергией E > U_m частично отражаются от барьера, а частицы с E < U_m частично проникают через барьер. Для того, чтобы убедиться в этом, рассмотрим совсем простой барьер, изображенный на Рис.3. Его можно рассматривать, как идеализацию ПБ, изображенного на Рис.2. Значение потенциальной энергии U(x) здесь всюду равно нулю, кроме области: . В областях I и III U(x) = 0, а в области II U(x) = U_m.

Можно представить себе, что такой барьер возникает в результате плавной деформации ПБ на Рис.2. Будем искать стационарные состояния частицы, движущейся в поле этого барьера. Обозначая потенциальную энергию через U(x), получаем стационарное уравнение Шредингера:

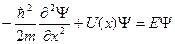(II.64)

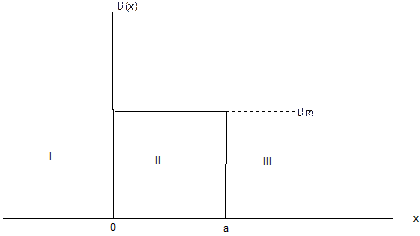
Рис. 3. Идеализация потенциального барьера.

В областях I и III U(x) = 0, поэтому:

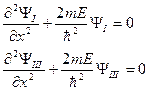(II.65)

В области II U(x) ≠ 0:

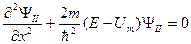(II.66)

Введем обозначения:

,

.

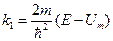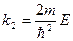Тогда получаем для каждой из трех областей стационарное уравнение Шредингера:

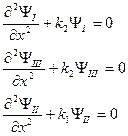(II.67)

Процесс взаимодействия частиц с барьером будет выглядеть следующим образом. Некоторые частицы будут отражаться от барьера в точке х = 0, и некоторые в точке х = а. В то же время какая-то часть частиц пройдет в этих точках сквозь барьер. Этот процесс схематически показан на Рис.4.

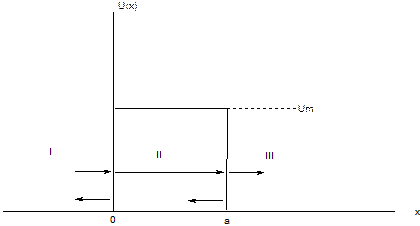
Рис. 4. Прохождение частицы через идеализированный потенциальный барьер.

Решение в этих трех областях может быть найдено в следующем виде. Для первой области:

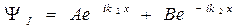(II.68)

Первый член в этой формуле соответствует движению вдоль оси Ох в положительном направлении, а второй – движению в противоположном направлении. Точно также для областей II и III имеем:

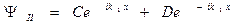
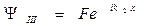(II.69)

Введем следующие обозначения:

| A |² – интенсивность падающей волны

| В |² – интенсивность отраженной волны

| C |² – интенсивность внутри барьера вдоль оси Ох

| D |² – интенсивность волны, отраженной внутри барьера

| F |² – интенсивность прошедшей сквозь барьер волны

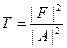- вероятность того, что частица прошла барьер (коэффициент прозрачности барьера)

Чтобы решение трех уравнений можно было рассматривать как предел решения одного уравнения при переходе от плавного изменения U(x) к скачкообразному, нужно, чтобы эти решения в точках х = 0 и х = а удовлетворяли граничным (краевым) условиям, таким, что волновые функции и их первые производные в этих точках слева и справа равны. То есть

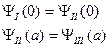
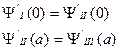(II.70)

Подставляя (II.68), (II.69) и их производные в (II.70), получаем:

A + B = C + D

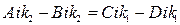(II.71)

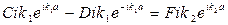
Поделим все уравнения (II.71) на А:

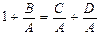
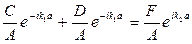(II.72)

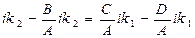
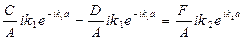
В системе уравнений (II.72):

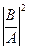- вероятность отражения от барьера (R – коэффициент отражения)

- вероятность проникновения в барьер

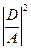- вероятность отражения от второй стенки барьера

Решая систему уравнений, получаем:

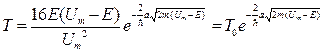(II.73)

Отсюда видно, что Т уменьшается с ростом массы m и увеличением ширины а ПБ. Из закона сохранения числа частиц R + T = 1. Из выражения для Т видно, при Е < U_m выражение под корнем положительно и частицы проходят сквозь барьер. Очевидно, что туннельный эффект имеет заметное значение лишь при тех случаях, когда Т не очень мал, т.е. когда

Из этого выражения видно, что с туннельным эффектом можно встретиться только в области микроскопических явлений. Так, для a = 1 см, получаем, что 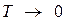. Парадоксальность туннельного эффекта состоит в том, что частица внутри ПБ при E < U_m должна иметь отрицательную кинетическую энергию, поскольку при U(x) > E, 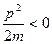. Но это бессмысленно, так как p – действительная величина. Однако, этот парадокс устраняется, если вспомнить, что одновременное знание кинетической и потенциальной энергии означает одновременное знание координаты частицы и ее импульса. А это в квантовой механике невозможно по принципу неопределенности Гейзенберга. Для облегчения понимания туннельного эффекта можно вспомнить, что в волновой оптике световое поле при полном отражении проникает в среду, от которой происходит отражение, и если это тонкая пластинка, то свет частично проходит через нее. Подтверждением работоспособности представлений о туннельном эффекте является объяснение с их помощью широко известного явления холодной эмиссии электронов в металлах и множества других явлений.

Поиск по сайту: