 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Оператор – это правило, с помощью которого одна функция превращается в другую
Понятие оператора в квантовой механике очень тесно связано с понятием среднего значения физической величины, которая в свою очередь требует введения нескольких терминов. Оператор действует на функции, находящиеся справа от него. Пусть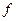 
– некоторая физическая величина, характеризующая состояние квантовой системы. Значения, которые может принимать 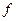, называются ее собственными значениями. Совокупность собственных значений образует спектр собственных значений. Дискретный спектр отвечает финитному движению, а непрерывный спектр соответствует инфинитному (неограниченному) движению. Рассмотрим случай дискретного спектра. Собственные значения величины 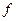обозначим 
, где 
Обозначим волновую функцию системы в состоянии, для которого 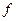имеет собственные значения , как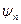 
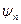. называется собственной функцией данной величины 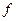. Все собственные функции нормированы 
. Волновая функция может быть разложена по собственным функциям любой физической величины. Система функций, по которой производится разложение, называется полной.
В общем случае произвольного состояния волновая функция может быть представлена в виде
(II.2)
Коэффициент 
соответствует вероятности появления 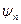. Поэтому
(II.3)
Можно показать, что
(II.4)
– это символ Кронекера
Таким образом, 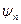ортонормированны. Итак, вернемся к операторам. В квантовой механике каждая наблюдаемая физическая величина (координата, импульс, момент импульса) представляется линейным оператором и среднее значение этой величины, наблюдаемой в квантовом состоянии 
, задается интегралом вида
(II.5)
Подобного типа интегралы, широко встречающиеся в квантовой механике, часто обозначают специальным образом:
(II.6)
и называются дираковскими по имени введшего их выдающегося физика Поля Дирака.
В квантовой механике есть два типа основополагающих операторов – это оператор координаты 
(
или 
) и оператор импульса 
. В частности, оператор координаты действует на произвольную функцию по простому правилу: 
, то есть просто переводит в произведение 
.
Оператор любой функции, зависящей только от координат 
, действует аналогично
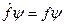
Оператор импульса, например,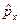 
переводит волновую функцию в ее частную производную по координате 
и одновременно умножает на 
, то есть
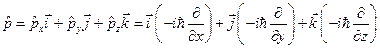(II.7)
Результатом действия оператора на волновую функцию является вектор с компонентами
Все остальные операторы получаются из соответствующих выражений классической механики заменой по указанным правилам координат и импульсов на отвечающие им операторы.
Отметим следующие свойства операторов – линейность и эрмитовость.
Поиск по сайту: