Гармонический осциллятор

Гармоническим осциллятором называется малое колебание периодического движения около устойчивого положения равновесия, отвечающего минимуму потенциальной энергии колеблющейся системы:U(q)→min.

Отклонение от положения равновесия q=q₀ приводит к возникновению силы , стремящейся вернуть систему в положение равновесия. q₀ – положение равновесия. Разложение в ряд Тейлора в окрестности точки дает:

(I.30)

По определению =0 в положении равновесия (точка минимума энергии.)

Выбираем начало отсчета так, что , тогда:

(I.31)

Обозначим x = q-q₀ – смещение из положения равновесия и определим k как

(I.32)

Тогда:

(I.33)

Кинетическая энергия при замене обобщенной скорости на скорость вдоль координаты х запишется:

(I.34)

А функция Лагранжа будет такой:

(I.35)

Находим уравнение Лагранжа для гармонического осциллятора:

(I.36)

Это линейное дифференциальное уравнение второго порядка имеет два независимых решения и , так что его общее решение или

(I.37)

Так как , сравнивая эти два выражения для x, получаем

(I.38)

a – амплитуда колебаний,

– начальная фаза колебаний, зависящая от выбора начала отсчета,

– циклическая частота

, где – частота колебания

(I.39)

То есть частота является основной характеристикой колебаний, не зависящей от начальных условий, она полностью определяется свойствами механической системы как таковой. Найдем, чему равна полная энергия Е классического гармонического осциллятора:

(I.40)

Так как , то:

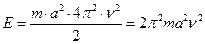(I.41)

Таким образом, полная энергия Е классического гармонического осциллятора является величиной, зависящей от его собственной частоты.

Поиск по сайту: