Консервативный гармонический осциллятор

В качестве модели консервативного гармонического осциллятора возьмём груз массы m, закреплённый на пружине жесткостью k.

Пусть x — это смещение груза относительно положения равновесия. Тогда, согласно закону Гука, на него будет действовать возвращающая сила:

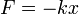
Используя второй закон Ньютона, запишем

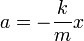
Обозначая 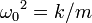и заменяя ускорение a на вторую производную от координаты по времени 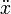, напишем:

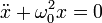
Это дифференциальное уравнение описывает поведение консервативного гармонического осциллятора. Коэффициент ω₀ называют циклической частотой осциллятора. (Здесь имеется в виду круговая частота, измеряющаяся в радианах в секунду. Чтобы перевести её в частоту, выражающуюся в Герцах, надо разделить круговую частоту на 2π)

Будем искать решение этого уравнения в виде:

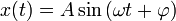
Здесь A — амплитуда, ω — частота колебаний (пока не обязательно равная собственной частоте), — начальная фаза.

Подставляем в дифференциальное уравнение.

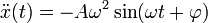
Амплитуда сокращается. Значит, она может иметь любое значение (в том числе и нулевое — это означает, что груз покоится в положении равновесия). На синус также можно сократить, так как равенство должно выполняться в любой момент времени t. И остаётся условие на частоту колебаний:

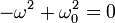
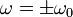
Отрицательную частоту можно отбросить, так как произвол в выборе этого знака покрывается произволом выбора начальной фазы.

Общее решение уравнения записывается в виде:

,

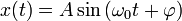где амплитуда A и начальная фаза — произвольные постоянные. Эта запись исчерпывает все решения дифференциального уравнения, так как позволяет удовлетворить любым начальным условиям (начальному положению груза и его начальной скорости).

Итого, консервативный гармонический осциллятор может совершать чисто гармонические колебания с частотой, равной его собственной частоте, с амплитудой любой величины и с произвольной начальной фазой.

№2

Энтропи́я (от греч. ἐντροπία — поворот, превращение) — понятие, впервые введённое в термодинамике для определения меры необратимого рассеивания энергии. Термин широко применяется и в других областях знания: в статистической физике — как мера вероятности осуществления какого-либо макроскопического состояния; в теории информации как мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса).

Третье начало термодинамики (теорема Нернста) — физический принцип, определяющий поведение энтропии при абсолютном нуле температуры. Является одним из постулатов термодинамики.

Третье начало термодинамики может быть сформулировано так:

«Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система».

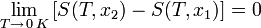
или

где x — любой термодинамический параметр.

Заметим, что третье начало термодинамики относится только к равновесным состояниям.

Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть, определяется не сама энтропия, а только её изменение):

,

Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что невозможно всю внутреннюю энергию системы превратить в полезную работу.

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

Существуют несколько эквивалентных формулировок второго начала термодинамики:

• Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему» (такой процесс называется процессом Клаузиуса).

• Постулат Томсона: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).

Билет 18

№1

Амплиту́да — максимальное значение смещения или изменения переменной величины при колебательном или волновом движении. Неотрицательная скалярная величина, измеряется в единицах, зависящих от типа волны или колебания.

Фа́за колеба́ний — аргумент периодической функци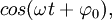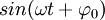и или 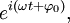описывающей гармонический колебательный процесс (ω— угловая частота, t — время, — начальная фаза колебаний, то есть фаза колебаний в начальный момент времени t = 0).

Фаза обычно выражается в угловых единицах (радианах, градусах) или в циклах (долях периода):

1 цикл = 2π радиан = 360°

Строго говоря, этот термин относится только к колебаниям, но его также применяют и к другим периодическим и квазипериодическим процессам.

Частота́ — физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени. Стандартные обозначения в формулах — , 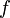или . Единицей частоты в Международной системе единиц (СИ) в общем случае является герц (Гц, Hz). Величина, обратная частоте, называется периодом.

№2

Необратимые процессы, физические процессы, которые могут самопроизвольно протекать только в одном определённом направлении. К ним относятся: процессы диффузии, теплопроводности, термодиффузии, вязкого течения, расширения газа в пустоту и т.п. Все Н. п. являются неравновесными процессами. В замкнутых системах Н. п. сопровождаются возрастанием энтропии. В открытых системах (которые могут обмениваться энергией или веществом с окружающей средой) при Н. п. энтропия может оставаться постоянной или даже убывать за счёт обмена энтропией с внешней средой. Однако во всех случаях остаётся положительным производство энтропии, т. е. её возрастание в системе за единицу времени из-за наличия Н. п.

Предположим, что рассматриваемое тело может обмениваться теплотой лишь с N бесконечными тепловыми резервуарами, внутренняя энергия которых столь велика, что при рассматриваемом процессе температура каждого остаётся строго постоянной. Предположим, что над телом был совершён произвольный круговой процесс, то есть по окончании процесса оно находится абсолютно в том же состоянии, что и в начале. Пусть при этом за весь процесс оно заимствовало из i-го резервуара, находящегося при температуре T_i, количество теплоты Q_i. Тогда верно следующее неравенство Клаузиуса:

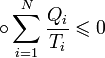
Здесь обозначает круговой процесс. В общем случае теплообмена со средой переменной температуры неравенство принимает вид

Здесь δ Q (T) — количество теплоты, переданное участком среды с (постоянной) температурой T. Это неравенство применимо для любого процесса, совершаемого над телом. В частном случае квазистатического процесса оно переходит в равенство. Математически это означает, что для квазистатических процессов можно ввести функцию состояния, называемую энтропией, для которой

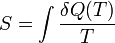
Билет 19

№1

Поиск по сайту: