Физический смысл работы

Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:

A ₁₂ = T ₂ - T ₁

№2

В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана:

n = n ₀exp(- mgh / kT)

где n - концентрация молекул на высоте h, n ₀ - концентрация молекул на начальном уровне h = 0, m - масса частиц, g - ускорение свободного падения, k - постоянная Больцмана, T - температура.

Билет 12

№1

В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует следующее определение: консервативные силы — такие силы, работа по любой замкнутой траектории которых равна 0.

Потенциальная энергия — работа, которую необходимо совершить, чтобы перенести тело из некой точки отсчёта в данную точку в поле консервативных сил.

Потенциальная энергия отсчитывается от некой точки пространства, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной точки называется нормировкой потенциальной энергии. Понятно также, что корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тел, но не от пути их перемещения. Такие силы называются консервативными.

К примеру, потенциальная энергия тела вблизи поверхности Земли рассчитывается по формуле 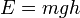, где m — масса тела, g - величина ускорения свободного падения, h — высота, за ноль принимается поверхность Земли.

№2

степень свободы - минимальное число переменных, описывающих перемещение молекулы в пространстве.

Теорема:

Если система молекул находится в равновесии при температуре Т, то Wk движения молекул распределится равномерно по степеням свободы, причем каждая ст. свободы обладает энергией 1\2kT.

Теплово́е движе́ние — процесс хаотического (беспорядочного) движения частиц, образующих вещество. Чаще всего рассматривается тепловое движение атомов и молекул.

(……….)

Билет 13

№1

Закон сохранения механической энергии — механическая энергия консервативной механической системы сохраняется во времени. Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может никуда исчезнуть.

№2

Билет 14

№1

Силы трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.

№2

Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нём обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии.

Билет 15

№1

Закон сохранения энергии — основной закон природы, заключающийся в том, что энергия изолированной (замкнутой) системы сохраняется во времени. Другими словами, энергия не может возникнуть из ничего и не может в никуда исчезнуть, она может только переходить из одной формы в другую. Закон сохранения энергии встречается в различных разделах физики и проявляется в сохранении различных видов энергии. Например, в классической механике закон проявляется в ]] закон сохранения энергии называется первым началом термодинамики и говорит

№2 \

Вероятность (вероятностная мера) — мера достоверности случайного события. Оценкой вероятности события может служить частота его наступления в длительной серии независимых повторений случайного эксперимента. Согласно определению П. Лапласа мерой вероятности называется дробь, числитель которой есть число всех благоприятных случаев, а знаменатель - число всех возможных случаев.

Функция статистического распределения (функция распределения в статистической физике) — одно из основополагающих понятий статистической физики. Знание функции распределения полностью определяет вероятностные свойства рассматриваемой системы.

Механическое состояние любой системы однозначно определяется координатами q_i и импульсами p_i ее частиц (i=1,2,…, d; d — число степеней свободы системы). Набор величин и образуют фазовое пространство. Вероятность нахождения системы в элементе фазового пространства (с точкой q, p внутри) дается формулой:

Функцию называют полной функцией статистического распределения (или просто функцией распределения). Фактически она представляет из себя плотность изображающих точек в фазовом пространстве.

Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, т. е. её отклонения от математического ожидания. Обозначается D [ X ] в русской литературе и (англ. variance) в зарубежной. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом.

Пусть — случайная величина, определённая на некотором вероятностном пространстве. Тогда

где символ M обозначает математическое ожидание.

Билет 16

№1

В классической механике, гармонический осциллятор — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука):

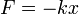
где k — положительная константа, описывающая жёсткость системы.

Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

№2.

Случа́йное собы́тие — подмножество исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.

Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом . Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом Ω.

Вероятность (вероятностная мера) — мера достоверности случайного события. Оценкой вероятности события может служить частота его наступления в длительной серии независимых повторений случайного эксперимента. Согласно определению П. Лапласа мерой вероятности называется дробь, числитель которой есть число всех благоприятных случаев, а знаменатель - число всех возможных случаев.

Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия.

Определение 1. Пусть задано вероятностное пространство , и на нём определена случайная величина . В частности, по определению, X является измеримым отображением измеримого пространства в измеримое пространство , где обозначает борелевскую сигма-алгебру на . Тогда случайная величина X индуцирует вероятностную меру на следующим образом:

Мера называется распределением случайной величины X.

Сре́днее значе́ние — числовая характеристика множества чисел или функций; — некоторое число, заключённое между наименьшим и наибольшим из их значений.

Исходным пунктом становления теории средних величин явилось исследование пропорций школой Пифагора. При этом не проводилось строгого различия между понятиями средней величины и пропорции. Значительный толчок развитию теории пропорций с арифметической точки зрения был дан греческими математиками – Никомахом Герасским (конец I – начало II в. н.э.) и Паппом Александрийским (III в. н.э.). Первым этапом развития понятия средней является этап, когда средняя стала считаться центральным членом непрерывной пропорции. Но понятие средней как центрального значения прогрессии не дает возможности вывести понятие средней по отношению к последовательности n членов, независимо от того, в каком порядке они следуют друг за другом. Для этой цели необходимо прибегнуть к формальному обобщению средних. Следующий этап – переход от непрерывных пропорций к прогрессиям – арифметической, геометрической и гармонической.^[1]

.

Билет 17

№1

Поиск по сайту: