Линейный вариационный метод, уравнения Рутаана

В квантово-химической литературе он известен больше как метод МО ЛКАО, что означает “ Молекулярные орбитали в виде линейных комбинаций атомных орбиталей ”. Такой способ решения уравнений Хартри-Фока был предложен Рутааном. И по существу его правильно называть методом Хартри-Фока-Рутаана. Оба эти названия (МО ЛКАО и Хартри-Фока-Рутаана) до сих пор широко используются в литературе.

Но, в связи с использованием в современных программных комплексах обозначений метода Хартри-Фока-Рутаана или МО ЛКАО как UHF или RHF (ROHF), названия МО ЛКАО и Хартри-Фока-Рутана постепенно заменяются этими новыми названиями. Это связанно с тем, что в современной квантовой химии исследователи используют готовые программные комплексы и, естественно, мало задумываются над сутью этих методов, их физическим смыслом.

Когда мы рассматривали теорему Купменса, мы уже фактически освободились от спиновых функций.

Перепишем эту систему уравнений для системы из N = 2n электронов с использованием кулоновского и обменного операторов. Причем рассматриваем случай замкнутых оболочек:

(III.75)

Даже расчет молекулярного иона H₂⁺ сложен, хотя можно получить довольно точное решение. Расчет движения одного электрона в поле Li₂⁺ намного сложнее, так как возникает вопрос о выборе потенциалов атомных остатков. Либо потенциал сложен, либо приближение грубое. Для отыскания нулевого приближения мы будем стараться выбрать пробную функцию так, чтобы она как можно точнее соответствовала физической картине движения электрона в молекуле и прежде всего правильно отражала геометрическое расположение атомов в ней. Наибольшее распространение получила пробная функция в виде ЛКАО.

Как мы говорили ранее, в методе Хартри-Фока сначала берется пробная волновая функция. Она подставляется в кулоновский и обменный интегралы, что позволяет считать гамильтониан известным. Затем решается система уравнений и находится новая функция. Теперь уже она берется в качестве пробной функции. Находится новая функция и т.д. до тех пор, пока не будет получено самосогласованное решение. Помимо прочих параметров, чем удачнее выбор пробной волновой функции, тем быстрее и будет получен результат. Согласно линейному вариационному методу, одноэлектронная функция пространственных координат представляется в виде линейной комбинации известных функций

(III.76)

Функции считаются нормированными, взаимной ортогональности их требовать пока не будем. Пока коротко рассмотрим, как каждая из таких функций составляется. То есть это предварительное рассмотрение для лучшего понимания физического смысла, заложенного в получаемые уравнения. Для каждого атома в молекуле, основываясь на его электронной конфигурации в свободном состоянии, вводится одна или несколько волновых функций -атомных орбиталей. Центры этих атомных функций совмещаются с ядрами молекул. Варьируются коэффициенты перед АО, то есть c_ka в нашей формуле. Такой вид представления МО в виде ЛКАО предложил Рутаан в 1950 г. для систем с замкнутыми оболочками и в 1960 г. для систем с открытыми оболочками. Эта идея оказалась очень плодотворной. В самом деле, с помощью такого разложения можно добиться того, что электрон должен ощущать влияние потенциала атомного ядра преимущественно вблизи этого ядра. Допустим, что молекула состоит из нескольких в общем случае различных атомов A, B, C и т.д. Очевидно, что один из электронов молекулы, находясь вблизи ядра А, испытывает наиболее сильное влияние со стороны именно этого ядра и окружающих его электронов, влияние же частиц остальных атомов незаметно. Очевидно, также, что около каждого ядра электроны располагаются так, чтобы по возможности компенсировать его положительный заряд. Таким образом находясь около ядра атома А, электрон попадает примерно в ту же обстановку, в которой он был бы в свободном атоме. Поэтому и естественно описывать в этом случае его состояние такой волновой функцией, которая была бы у него в свободном атоме. Находясь между ядер атомов, электрон испытывает влияние обоих атомных остатков, и поэтому можно описать его состояние линейной комбинацией атомных функций обоих этих атомов. Итак, вернемся к системе уравнений Хартри-Фока и подставим в уравнение (III.75) разложение (III.76).

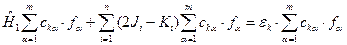(III.77)

Перепишем его таким образом:

(III.78)

Умножив (III.78) на f^*_b и проинтегрировав по x, y, z, получим

(III.79)

где b = 1, 2, 3,................m; a = 1, 2, 3,………………n

Система (III.79) представляет собой “nm” уравнений для определения “nm” величин с_ka. Внешне она выглядит как однородная система алгебраических уравнений для с_ka и она являлась бы таковой, если бы операторы и сами не содержали неизвестных коэффициентов с_ka. Если вместо операторов и подставить их явные выражения:

,

а вместо и их разложения, то получим очень сложную нелинейную систему уравнений относительно с_ka, решить которую практически невозможно. Поэтому упростить нашу систему можно, если мы перепишем ее с оператором Фока в следующем виде:

………………………………………………………..

(III.80)

здесь .

Мы опустили значок “k” в с_ka и . Дело в том, что в (III.79) и (III.80) – собственные значения и они тоже неизвестны. Коэффициенты же этих уравнений, не содержат значка “k”. Величины e определяются из векового уравнения, которое является условием существования нетривиального решения системы (III.79).

(III.81)

Это алгебраическое уравнение m- й степени относительно e корни, которого определяет “m” значений e₁, e₂, e₃,…………, e_m. Для каждого значения e_k после его подстановки в (III.80) мы получаем набор m значений c_ka: c_k1, c_k2, c_k3,....... c_km, с помощью которых построим k- ю орбиталь:

, (III.82)

то есть получаем с_1a и строим , затем с_2a и строим и так до с_ma ® . Таким образом мы получим “m” различных орбиталей. Число орбиталей должно быть достаточным для размещения на них всех электронов. Уравнения Рутаана, называемые часто уравнениями Хартри-Фока-Рутаана, записываются кратко следующим образом:

(III.83)

Эти уравнения являются базовыми в современной квантовой химии. Их можно либо упрощать и получать уравнения, реализующие полуэмпирические методы, либо усложнять и получать уравнения, учитывающие энергию электронной корреляции, которые предназначены для самых точных расчетов. Эти методы рассматриваются в спецкурсе «Избранные главы квантовой химии».

Поиск по сайту: