Дифференциальные уравнения движения вязкой жидкости. Граничные условия

Рассмотрим общий случай гидродинамики вязких жидкостей. Для получения уравнения движения такой жидкости используем общие уравнения гидродинамики в напряжениях в проекциях на оси координат [1]

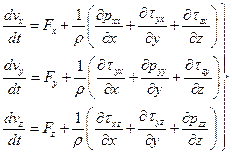(4.1)

В этих уравнениях заданы проекции напряжения массовых сил , , и (для несжимаемой жидкости) плотность r. Требуется найти три проекции скорости , , , нормальные и касательные напряжения, т.е. компоненты матрицы напряжений. В силу свойств парности касательных напряжений достаточно отыскать три касательных напряжения, например, 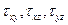. К этим трем уравнениям, в которые входят девять неизвестных величин, присоединяется уравнение неразрывности

.

Таким образом, эта система уравнений получается незамкнутой; в ней число неизвестных превышает число уравнений. Чтобы найти эти неизвестные, необходимо составить дополнительные уравнения, связывающие возникающие в жидкости касательные и нормальные напряжения с ее скоростями. При этом надо учесть, что вязкость приводит к возникновению не только касательных напряжений, но и к изменению нормальных напряжений по сравнению с невязкой жидкостью.

Рассмотрим течение, создаваемое движущейся со скоростью стенкой (рис.15), называемое плоским сдвиговым течением, так как частицы в нем испытывают деформации сдвига, характеризуемые относительной скоростью сдвига

.

В вязкой жидкости в таком течении возникают касательные напряжения

.

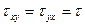В соответствии с законом Ньютона о связи касательных напряжений со скоростями жидкости,

, т.е. . (4.2)

Будем считать, что формула Ньютона (4.2), полученная для частного случая одномерного течения, справедлива и в общем случае трехмерного потока. Это позволяет ввести обобщенную гипотезу Ньютона о том, что напряжения, зависящие от вязкости, пропорциональны соответствующим относительным скоростям угловых деформаций жидкой частицы. При этом коэффициент пропорциональности остается таким же, как и в формуле (4.2), т.е. 2 m. В соответствии с этой гипотезой связь между матрицей напряжений и матрицей скоростей деформаций имеет вид

. (4.3)

Такая связь между матрицами при обеспечивает переход к зависимостям для невязкой жидкости. В результате нормальное напряжение по любой оси можно представить в виде двух слагаемых

(4.4)

Первое слагаемое в этих выражениях– давление в вязкой жидкости; второе слагаемое непосредственно учитывает влияние вязкости. Найдем среднее арифметическое от величин нормальных напряжений по трем взаимно перпендикулярным направлениям, учтя при этом уравнение неразрывности

(4.5)

где p – гидродинамическое давление. Отсюда следует, что давление в вязкой несжимаемой жидкости – это взятое с обратным знаком среднее арифметическое из нормальных напряжений по трем взаимно перпендикулярным направлениям. Знаком минус в этом уравнении учтено, что давление соответствует сжимающим нормальным напряжениям, направленным против внешней нормали.

Для получения уравнений движения вязкой жидкости подставим в правую часть их первого уравнения значения нормальных и касательных напряжений согласно принятой гипотезе. В проекции на ось x, учитывая выражения для e и q, получим

(4.6)

где D - оператор Лапласа. При выводе этого выражения изменен порядок дифференцирования и учтено уравнение неразрывности. С учетом (4.6) получим уравнения движения вязкой жидкости, называемые уравнениями Навье-Стокса, имеющие в векторной форме вид

(4.7)

или в проекциях на оси координат

Эти уравнения отличаются от уравнений Эйлера движения невязкой жидкости членами, характеризующим силы вязкости, и переходят в них при m =0. Уравнение (4.7) – нелинейное дифференциальное уравнение второго порядка в частных производных; нелинейность обусловлена членом с конвективным ускорением. Его решение следует подчинить начальным и граничным условиям. Все соображения о начальных условиях для течения невязкой жидкости сохраняют свою силу и для вязкой жидкости. Принципиально новым является лишь изменение граничного условия на твердых границах потока.

При обтекании тела потоком вязкой жидкости выполняется граничное условие прилипания (приводилось при рассмотрении закона Ньютона [1]). Оно заключается в том, что наряду с условием непротекания и безотрывного обтекания , на поверхности тела выполняется условие прилипания жидкости, т.е. касательная составляющая скорости . В сумме два эти условия дают .

Выполнение условия прилипания не зависит от материала поверхности и степени чистоты его обработки. Оно одинаково выполняется при обтекании любых поверхностей. В настоящее время это условие является общепринятым в гидромеханике вязкой жидкости. Оно может нарушаться лишь в потоках очень разреженных газов.

В случае движения тела в покоящейся жидкости также соблюдается условие прилипания. Частицы жидкости, прилегающие к телу, увлекаются им (рис.15) и скорость частиц жидкости, прилегающих к поверхности тела равна скорости движения тела .

Поиск по сайту: