Потенциал скорости. Уравнение Лапласа

Безвихревым называется такое движение жидкости, при котором отсутствуют угловые скорости вращения частиц жидкости, т.е. . Несмотря на то, что из-за вязкости течение реальной жидкости практически всегда вихревое, изучение безвихревых течений представляет большой практический интерес. В ряде случаев вязкость реальных жидкостей проявляется в ограниченных областях, как правило, вблизи твердых стенок или тел, движущихся в жидкости. Остальная часть потока может быть рассмотрена с позиций безвихревого движения, что значительно облегчает его теоретическое исследование. Изучение волновых движений, расчет волнового сопротивления судна также базируется на теории безвихревого движения.

В соответствии с формулами для проекций угловой скорости вращения частиц [1], условие выполняется, если

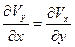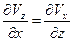, , . (2.1)

Последние зависимости обусловливают существование функции 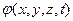, называемой потенциалом скорости, который связан со скоростью следующим образом

, (2.2)

тогда проекции скорости на оси координат можно выразить в виде частных производных от потенциала по координатам:

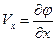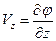, , . (2.3)

В общем случае проекция скорости на произвольное направление

.

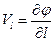Функция j тождественно удовлетворяет условиям (2.1), в чем нетрудно убедиться, подставляя в них значения скоростей, выраженные через потенциал j:

, , .

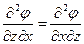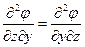Так как производная от функции не зависит от порядка дифференцирования, эти равенства являются тождествами и выполняются при безвихревом движении. Таким образом, если движение безвихревое, то существует потенциал скорости j. Отсюда второе название безвихревого движения – потенциальное течение.

При существовании потенциала скорости решение задач гидромеханики значительно упрощается, так как вместо определения трех функций – V_x, V_y, и V_z – достаточно найти только одну - j, которая целиком определяет кинематику безвихревого потока.

Основное уравнение, из которого можно определить потенциал скорости j, получается из уравнения неразрывности в дифференциальной форме [1]

,

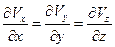куда вместо проекций скорости следует подставить их выражения через потенциал скорости (2.3). В результате

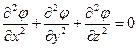(или 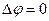). (2.4)

Полученное уравнение в частных производных называется уравнением Лапласа. Из этого уравнения может быть найден потенциал скорости j при заданных начальных и граничных условиях [1].

Поиск по сайту: