АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Обтекание кругового цилиндра

Читайте также:
  1. ГЛАВА V. Обтекание тел потоком вязкой жидкости.
  2. Закон Био и Савара. Магнитное поле кругового тока.
  3. Магнитное поле кругового тока
  4. Обтекание кругового цилиндра с циркуляцией.
  5. Обтекание сферы.

Поперечное обтекание бесконечного кругового цилиндра поступательным потоком является плоскопараллельным течением, которое можно свести к рассмотрению обтекания круга в плоскости xy.

Расчет обтекания цилиндра выполняется методом сложения простейших потенциальных потоков – поступательного потока вдоль оси x (1.1.8) и плоского диполя в начале координат (1.1.12).

Потенциал суммарного потока имеет вид

,

но его удобнее записать в полярной системе координат rf

. (3.)

Функцию тока этого течения также можно получить сложением функций тока составляющих (1.1.9) и (1.1.13).

. (3.)

Приравнивая функцию тока нулю, можно получить уравнение нулевой линии тока

.

У этого уравнения два решения, первое

дает прямую линию, совпадающую с осью x, второе

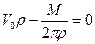(3.)

дает выражение для r

. (1.2.4)

Так как момент диполя и V0 – постоянные величины, то если обозначить

, (1.2.5)

то из (1.2.3) получим уравнение окружности радиусом r0 с центром в начале координат (рис.4).

 

 

Рис. 4

Если заменить эту линию тока твердым телом, то на его поверхности будет выполняться условие непротекания

,

так как нормаль к окружности - это ее радиус.

Таким образом, мы доказали, что потенциал (1.2.1) описывает обтекание кругового цилиндра потоком невязкой жидкости.

Выразим момент диполя через радиус цилиндра из (1.2.5):

,

тогда потенциал течения примет окончательный вид

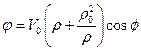. (1.2.6)

Из (37) можно получить выражения для скоростей Vr и Vf

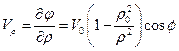, (1.2.7)

, (1.2.8)

откуда видно, что при r=r0, то есть на поверхности цилиндра,

, .

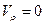Полная скорость на поверхности цилиндра

,

при этом безразмерная скорость

, (1.2.9)

а значение коэффициент давления на цилиндре выражается формулой

. (1.2.10)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)