Поле скоростей и давлений, вызываемых прямолинейной вихревой трубкой

Поле скорости, вызванное прямолинейной бесконечной вихревой трубкой, выражается следующей зависимостью

, (1.9)

где h – расстояние от оси вихревой трубки до точки, в которой определяется скорость.

Очевидно, что картина течения жидкости в любой плоскости, перпендикулярной оси вихря, одинакова, то есть течение плоскопараллельное.

Для полубесконечного вихря, простирающегося от начала координат до бесконечности, вызванные скорости определяются по формуле

, (1.10)

то есть полубесконечный вихрь индуцирует вдвое меньшую скорость, нежели бесконечный. Поскольку согласно кинематической теореме Гельмгольца вихрь в жидкости не может кончаться, следует исходить из предположения, что начало координат соответствует границе твердого тела, с которого сходят полубесконечные вихревые трубки. Формула (1.10) используется в теории крыла.

Рассмотрим более подробно случай бесконечной вихревой трубки, находящейся в покоящейся жидкости. Вызванные ею скорости определяются зависимостью (1.9). Что же касается центра вихревой трубки h =0, то величина скорости в нем, определенная по этой формуле, окажется бесконечно большой. Поэтому распределение скоростей в области, непосредственно прилегающей к центру вихря, должно выражаться другой зависимостью, отвечающей условию конечности скорости в этой области.

Будем считать, что завихренность сосредоточена лишь в ядре вихря радиусом h=r_в, как на рис.8, где показано поперечное сечение вихревой трубки. Вне цилиндрической поверхности радиуса r_в (вне ядра вихря) движение жидкости безвихревое.

Если считать, что ядро вихря движется как единое целое (т.е. как твердое тело), то угловые скорости частиц жидкости в ядре можно считать постоянными , откуда вытекает, что распределение скоростей в ядре следует линейному закону.

(1.11)

Картина распределения скоростей в плоскости xy показана на рис.8; при 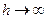, получаем 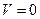, то есть жидкость вдали от вихря покоится, при h =0 скорость жидкости в центре вихря .

Исследуем поле давлений, вызываемых вихрем. Для этого нельзя использовать уравнение Бернулли, так как рассматриваемые точки лежат на разных линиях тока, но можно использовать другой интеграл уравнений движения невязкой жидкости – уравнение Эйлера

,

которое справедливо для любой пары точек в безвихревом потоке.

Согласно этому уравнению, выражение для давления вне ядра вихря в соответствии с (1.9)

,

где p₀ – давление в покоящейся жидкости.

Последнее выражение справедливо вплоть до границы вихревой трубки h=r_в. Полагая в нем h=r_в, получим давление на границе

. (1.12)

Из этой формулы видно, что по мере приближения к вихрю давление уменьшается.

Внутри ядра течение вихревое, и интеграл Эйлера неприменим. Поскольку закон распределения скоростей в ядре вихря известен (1.11), можно определить давление непосредственно из дифференциальных уравнений движения невязкой жидкости. Для плоскопараллельного установившегося движения, пренебрегая массовыми силами, можно этим уравнениям придать вид

;

.

Согласно рис.8, внутри ядра вихря

, .

На основании этого находим

, .

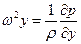Умножая первое слагаемое на dx, второе на dy и складывая их, получим

.

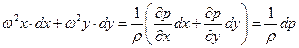Интегрируя последнее уравнение и подставляя выражение (1.12) на границе вихря для определения постоянной интегрирования, получим выражение для давления внутри вихревой трубки

. (1.13)

В центре вихря V_C =0, т.е.

. (1.14)

Как видно из рис.8, в среде, окружающей вихревую трубку, давление непрерывно уменьшается по мере приближения к оси вихря.

Поиск по сайту: