Интегралы Лагранжа и Эйлера

Из дифференциальных уравнений движения невязкой жидкости [1]

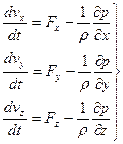(3.1)

можно получить не только интеграл Бернулли. Для случая безвихревого движения невязкой жидкости возможно получить еще два интеграла – уравнения Эйлера и Лагранжа.

Для их вывода преобразуем выражение ускорения 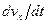. Произведем выкладки для плоского течения, а затем обобщим полученный результат на пространственный случай.

Запишем ускорение 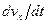через местную и конвективную составляющую, добавив и вычтя в этом выражении член :

.

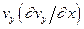Перегруппировав члены в правой части этого выражения, получим

.

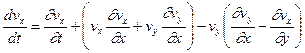В свою очередь

.

Используя выражение для проекции угловой скорости w_z, получим

.

С учетом сделанных преобразований, запишем проекции уравнения движения на ось x в виде

. (3.2 а)

Легко видеть, что для плоского течения . Обобщая этот вывод на пространственный случай течения, будем иметь

, (3.2 б)

. (3.2 с)

Уравнения (3.2 а-с), в которых в явной форме выделены кинематические особенности течения (угловые скорости) называются дифференциальными уравнениями в форме Громеко. В ряде случаев они более удобны для интегрирования, чем дифференциальные уравнения в форме Эйлера.

Для безвихревого течения жидкости справедливы следующие соотношения:

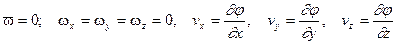. (3.3)

а также для массовых сил

, (3.4)

откуда потенциал массовых сил U получаем в виде .

Подставив равенства (3.3) и (3.4) в уравнения (3.2 а-с), учитывая, что

,

и перенося члены правой части в левую, будем иметь:

(3.5)

Из системы уравнений (3.5) следует, что сумма четырех слагаемых в квадратных скобках не зависит от координат, но является функцией времени. С учетом этого получим интеграл Лагранжа для неустановившегося потенциального течения

. (3.6)

Функция времени F(t), как правило, находится из граничных условий задачи.

Рассмотрим частный случай установившегося потенциального течения, в котором , а скорость и давление не зависят от времени

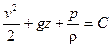, (3.7)

где постоянная 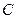одинакова для всех точек потока. Этот интеграл называется интегралом Эйлера. Его физический смысл тот же, что и для интеграла Бернулли: это выражение закона сохранения энергии.

Видно, что по форме интегралы Эйлера и Бернулли совпадают, но между ними, подчеркнем, имеется существенная разница: в интеграле Эйлера 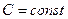для всего потока, а в интеграле Бернулли она постоянна лишь только вдоль линии тока.

Поиск по сайту: