АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Интерполяционный многочлен Лагранжа

Читайте также:
  1. Интегралы Лагранжа и Эйлера
  2. Індивідуальні завдання з теорії многочленів
  3. Метод неопределенных множителей Лагранжа
  4. Многочлен имеет степень на один меньше, чем разрядность вектора. Над многочленами вводятся три вида операций: сложение (аналогично «сложению по модулю 2»), умножение, деление.
  5. ПРИЛОЖЕНИЕ 5. КОМПЬЮТЕРНАЯ ПРОГРАММА ВЫРАВНИВАНИЯ ДИНАМИЧЕСКОГО РЯДА МНОГОЧЛЕНОМ РЯДА ФУРЬЕ
  6. Уравнения Лагранжа второго рода
  7. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА ПРИ НЕСТАЦИОНАРНОМ БАЗИСЕ

Пусть на отрезке [a,b] заданы (n+1) точка x0, x1, ¼, xn и значения функции f в этих точках.

Будем строить интерполяционный многочлен вида 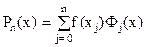, где - многочлены степени n, удовлетворяющие условиям

так как требуем, чтобы значения интерполяционного многочлена и значения функции f(x) совпадали в узлах интерполяции i, т.е. .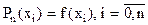

Тогда 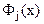можно искать в виде:

где 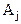- некоторая константа, которую найдем из условия 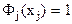, тогда

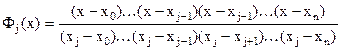
Если обозначить 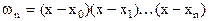и продифференцировать это выражение по х, полагая х=хj, то последнее выражение можно записать в виде:

,

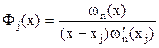где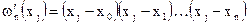

Таким образом, получим многочлен

,

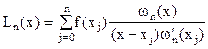который называется интерполяционным многочленом Лагранжа.

Пусть узлы интерполирования являются равноотстоящими, т.е. , если ввести новую переменную , то многочлен Лагранжа для равноотстоящих узлов запишется в виде

,

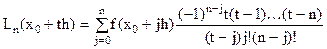т.к. .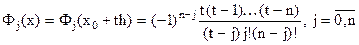

Интерполяционный многочлен Лагранжа имеет существенный недостаток: если при выбранном числе узлов выяснилось, что интерполяционный многочлен недостаточно точно находит значение функций в заданной точке, то при добавлении одного или нескольких узлов все вычисления необходимо проводить заново. В том случае, когда требуется найти не аналитическое выражение, а лишь его значение в некоторой точке, от этого недостатка можно избавиться, воспользовавшись интерполяционной схемой Эйткена.

По этой схеме значение интерполяционного многочлена Лагранжа находится путем последовательного применения единообразного процесса

x0 y0 x0-x        
x1 y1 x1-x L01(x)      
x2 y2 x2-x L12(x) L012(x)    
¼ ¼ ¼ ¼ ¼ ¼ ¼
xn yn xn-x Ln-1n(x) Ln-2n-1n(x) Ln-3¼n(x)¼ L01¼n(x)

где , , , .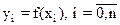

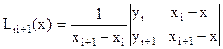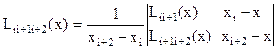Применяя эту схему, можно постепенно подключать все новые и новые узлы до тех пор, пока желаемая точность не будет достигнута.

Если все вычисления проведены точно, то интерполяционный многочлен Лагранжа совпадает с заданной функцией в узлах интерполирования. Однако он будет отличен от нее в остальных точках. Исключением является случай, когда сама функция f(x) является многочленом степени не выше n.

Оценка погрешности интерполяционного многочлена Лагранжа, если функция f(x) имеет на [a,b] непрерывные производные (n+1)-го порядка, имеет вид 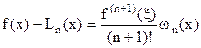, где x - некоторая точка [a,b] или .

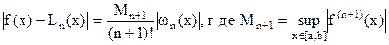Это выражение может служить оценкой отклонения полинома Лагранжа от f(x) в том случае, когда можно оценить .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)