Метод Данилевского. Суть метода в приведении векового определителя к нормальному виду Фробениуса:

Суть метода в приведении векового определителя к нормальному виду Фробениуса:

. (5.4)

Разложив определитель (5.4) по первой строке будем иметь:

. (5.5)

Известно, что преобразование подобия не изменяет характеристического многочлена матрицы А. Поэтому, удачно подобрав преобразование подобия, можно получить матрицу, собственный многочлен которой может быть выписан по ее виду.

Рассмотрим модификацию метода Данилевского удобную для численной реализации. Пусть задана матрица

(5.6)

с помощью преобразований подобия матрица (5.6) приводится к матрице имеющей нормальную форму Фробениуса:

(5.7)

Процесс приведения к нормальной форме Фробениуса:

I. Матрица А умножается справа на матрицу С₁, а слева на :

, (5.7)

В результате получаем матрицу , у которой (n-1) – й столбец имеет нужный нам вид.

II. На втором шаге матрица умножается справа на матрицу С₂, а слева на :

, (5.7)

В результате получаем матрицу 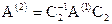, у которой (n-1) – й и (n-2) – й столбцы имеют тот же вид, что и соответствующие столбцы матрицы Фробениуса.

Продолжая этот процесс, после (n-1) – го шага получим матрицу , имеющую нормальную форму Фробениуса. Здесь предполагается, что , 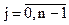отличны от нуля.

Собственный многочлен матрицы имеет вид:

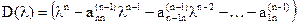, (5.8)

Корни многочлена (5.8) являются собственными значениями исходной матрицы А.

Если 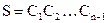, а - собственный вектор матрицы , то собственный вектор матрицы А определяется соотношением , т.е. для определения компонент собственного вектора имеем:

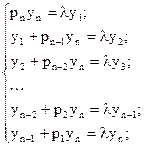(5.9)

Т.к. собственный вектор определяется с точностью до числового множителя, то можно считать, что . Таким образом решая систему (5.9) будем иметь:

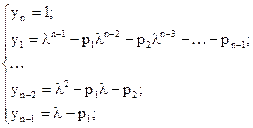(5.10)

Поиск по сайту: