 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Относительная погрешность суммы
 . Пусть
. Пусть 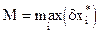 , а
, а  . Следовательно
. Следовательно 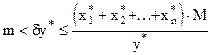
Замечание: на практике применяется верхняя оценка.
Правила вычисления погрешностей [1]:
1. Предельная абсолютная погрешность суммы или разности равна сумме предельных погрешностей.
2. Относительная погрешность суммы положительных слагаемых не превышает наибольшей из относительных погрешностей этих слагаемых.
3. Предельная относительная погрешность произведения или частного равна сумме предельных относительных погрешностей.
4. Предельная относительная погрешность степени и корня приближенного числа равна произведению предельной относительной погрешности этого числа на показатель степени.
Поиск по сайту: