 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод Крылова
Суть метода заключается в построении алгебраического образа. По виду которого можно было бы сразу записать собственный многочлен вещественной матрицы А.
Возьмем произвольный вектор  , согласованный по размерности с матрицей А, и по этому вектору будем составлять последовательность векторов
, согласованный по размерности с матрицей А, и по этому вектору будем составлять последовательность векторов  ,
,  , … до тех пор пока не встретится такой вектор
, … до тех пор пока не встретится такой вектор  , т.е. вектор являющийся линейной комбинацией предыдущих линейно независимых векторов.
, т.е. вектор являющийся линейной комбинацией предыдущих линейно независимых векторов.
Для определения номера m составляют максимально возможную линейную комбинацию, т.е. полагают m=n:
 (5.11)
(5.11)
Здесь  , при
, при  - координаты вектора
- координаты вектора 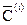 ,
,  . В результате для определения
. В результате для определения  имеем систему n – линейных алгебраических уравнений.
имеем систему n – линейных алгебраических уравнений.
Для случая линейной независимости векторов  , ¼,
, ¼,  полученную систему решают методом Гаусса. В том случае, когда линейно независимы только m первых векторов, находят m коэффициентов системы
полученную систему решают методом Гаусса. В том случае, когда линейно независимы только m первых векторов, находят m коэффициентов системы  .
.
Зная все значения коэффициентов  можно записать собственный многочлен матрицы А:
можно записать собственный многочлен матрицы А:  . Решив уравнение
. Решив уравнение 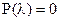 , найдем все собственные значения матрицы А.
, найдем все собственные значения матрицы А.
В том случае, когда найдены только m коэффициентов системы, можно записать многочлен  , который является делителем собственного многочлена матрицы А. Решив уравнение:
, который является делителем собственного многочлена матрицы А. Решив уравнение:  , найдем часть собственных значений матрицы А. Изменяя исходный вектор
, найдем часть собственных значений матрицы А. Изменяя исходный вектор  и проделав все вычисления заново, находим все оставшиеся собственные значения.
и проделав все вычисления заново, находим все оставшиеся собственные значения.
Собственный вектор  соответствующий собственному значению
соответствующий собственному значению  ищется в виде линейной комбинации линейно-независимых векторов:
ищется в виде линейной комбинации линейно-независимых векторов:
 ,
,
где коэффициенты  ;
;  , ¼,
, ¼,  .-
.-
Поиск по сайту: