АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод линеаризации данных по методу наименьших квадратов

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Методические основы
  3. I. Предмет и метод теоретической экономики
  4. II. Метод упреждающего вписывания
  5. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  6. II. Методы непрямого остеосинтеза.
  7. II. Проблема источника и метода познания.
  8. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ
  9. III. Методологические основы истории
  10. III. Предмет, метод и функции философии.
  11. III. Социологический метод
  12. III. УЧЕБНО – МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ПО КУРСУ «ИСТОРИЯ ЗАРУБЕЖНОЙ ЛИТЕРАТУРЫ К. XIX – НАЧ. XX В.»

Техника линеаризации данных применяется для подгонки кривых, позволяющих при преобразовании переменных получить линейную зависимость вида 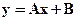. В таблице 1 приведены основные приемы линеаризации.

Таблица 1.

Таблица замены переменной для метода линеаризации данных

№ п/п Функция Линеаризованная форма Замена переменных и констант
1.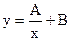
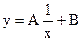
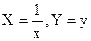
2.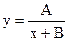
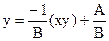
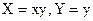
3.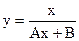
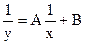
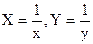
4.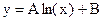
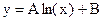
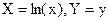
5.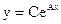
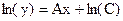
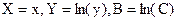
6.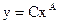

 

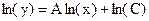
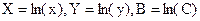
Пусть заданы N точек с различными абсциссами {xk}. Величина среднеквадратичной ошибки будет минимальной, когда каждая частная производная 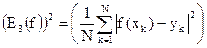по неизвестным (в данном случае неизвестные А и В) будет обращаться в нуль, т.е. А и В являются решением нормальной системы уравнений вида:

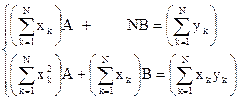(3.4)

Решая систему нормальных уравнений (3.4) находим искомые коэффициенты А и В.

Пример: Аппроксимировать таблично заданную функцию по пяти заданным точкам полиномом первой степени или построить линейную зависимость с помощью метода наименьших квадратов.

k          
xk          
yk         3.5

Решение:

1. Запишем нормальную систему для 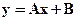- полинома первой степени:

,

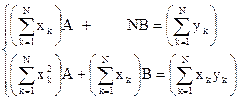где N = 5 – количество точек.

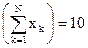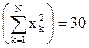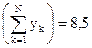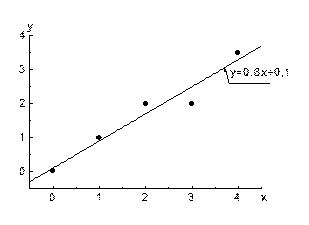
2. Вычислим все необходимые суммы:N=5, , , , 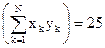. Таким образом, подставляя числовые значения сумм в нормальную систему и решая ее, относительно неизвестных получаем, что А=0,8 и В=0,1

3. Таким образом,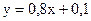

4. Проверяем полученный полином. Для наглядности построим исходные данные и полученную зависимость на графике:

Замечания:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)