Кусочно-кубические сплайны

Определение: Функция S(x) называется кубическим сплайном, если существует N кубических полиномов S_k(x) с коэффициентами s_k,0, s_k,1, s_k,2, s_k,3, которые удовлетворяют следующим условиям:

1. 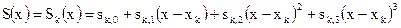, для

и , т.е. кубический сплайн состоит из кубических полиномов.

2. Кусочно-кубическое интерполирование задается совокупностью точек, т.е. 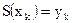для .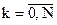

3. Кусочно-кубическое представление состояло из кривых, которые являются гладкими непрерывными функциями. Вторая и первая производные должны быть непрерывны: , , .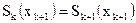

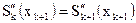Наиболее часто на практике используется кубический сплайн следующего вида: .

Для задания сплайна коэффициенты 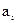, , , 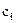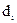- подбираются так, чтобы , а первая и вторая производные были непрерывными.

Леммы о сплайнах:

1. Смыкающий (чертежный) сплайн. Существует единственный кубический сплайн, который имеет первую производную с граничными условиями 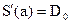, , т.е. смыкающий сплайн имеет определенный наклон в крайних точках.
2. Естественный сплайн. Существует единственный кубический сплайн со свободными граничными условиями , , 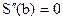т.е. сплайн допускает свободный наклон на краях для обеспечения положения, которое минимизирует осцилляцию кривой.
3. Экстраполяционный сплайн. Существует единственный кубический сплайн, который используется для экстраполирования по внутренним узлам, чтобы определить 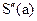по узлам х₁, х₂ и 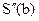по узлам х_N-1, х_N-2.
4. Сплайн, заканчивающийся параболой. Существует единственный кубический сплайн такой, что на интервале [x₀, x₁] и на интервале [x_N-1, x_N].
5. Сплайн с заданной кривизной в крайних точках. Существует единственный кубический сплайн с заданными значениями второй производной в крайних точках.

Поиск по сайту: