Интерполяционные и экстраполяционные формулы при равноотстоящих значениях аргумента

Пусть все узлы интерполирования х_i принадлежат отрезку [a,b], причем а=х₀, b=x_n.

Если точка интерполирования х принадлежит отрезку [a,b], то формула, приближающая функцию f в точке х, называется интерполяционной, а если х не принадлежит отрезку [a,b], то формула называется экстраполяционной.

Узлы интерполирования, лежащие ближе к точке интерполирования, оказывают большее влияние на интерполяционный многочлен, чем узлы, лежащие дальше. Поэтому целесообразно за и брать ближайшие к х узлы интерполирования и проводить сначала линейную интерполяцию по этим узлам, а затем постепенно привлекать следующие узлы таким образом, чтобы они возможно симметричнее располагались относительно точки. Полученные при этом поправки будут незначительными.

Пусть узлы интерполирования определены на [a,b] равномерно и заданы значения интерполируемой в этих узлах функции.Формула Ньютона для интерполирования вперед и экстраполирования назад

Пусть точка интерполирования х находится ближе к левому концу отрезка [a,b] или слева от него. Тогда интерполяционная формула Ньютона для интерполирования вперед и экстраполирования назад примет вид

,

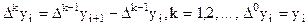где - новая переменная, - конечная разность k - го порядка.

Связь разностных соотношений и конечных разностей:

, , и т.д.

Остаток в этом случае имеет вид

.

Поиск по сайту: