Общие понятия. В инженерной практике часто используют совокупности точек, абсциссы которых различны, полученные в результате экспериментов

В инженерной практике часто используют совокупности точек, абсциссы которых различны, полученные в результате экспериментов. Назначение численных методов заключается в определении зависимости, которая связывает данный набор точек. Другими словами в этом случае численные методы определяют класс допустимых формул, коэффициенты которых должны быть определены. Существует множество различных типов функций, которыми можно воспользоваться. Рассмотрим класс линейных функций вида: . Все рассмотренные до этого методы позволяли получить полиномы, достаточно хорошо аппроксимирующие или интерполирующие данные при условии, что эти данные достаточно точны, т.е. точки получены, по крайней мере, с пятью знаками точности. Однако, часто в измерениях экспериментальная ошибка достаточно велика, т.е. истинное значение удовлетворяет равенству: 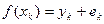, где 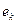- ошибка измерения.

Для того, чтобы определить насколько далеко от данных лежит кривая можно воспользоваться следующими нормами:

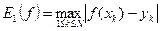- максимальная ошибка, (3.1)

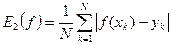- средняя ошибка, (3.2)

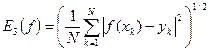- среднеквадратичная ошибка. (3.3)

Пример: Сравним ошибки для линейного приближения функции 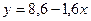по заданной таблице точек

Решение:

Вычислим все три вида ошибок:

.

.

.

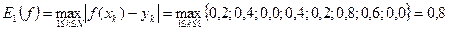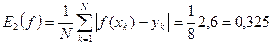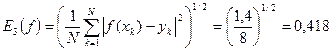Таким образом, построенная наилучшим образом линия определяется минимизацией одной из величин, заданных выражениями (3.1) – (3.2). В связи с тем, что третью норму легче минимизировать выбирают её.

Поиск по сайту: