АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Обратная задача теории погрешности

Читайте также:
  1. I. МЕХАНИКА И ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
  2. VI. Общая задача чистого разума
  3. XII. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ
  4. Активность личности, психоаналитические теории личности
  5. Антропологические теории мифа
  6. Антропологические теории ритуала
  7. Билет 2. Теории исторического развития
  8. Билет № 35 Проблема познания в философии. Основные направления в теории познания.
  9. Биография Ч. Дарвина. Основные его труды. Оценка теории Ч. Дарвина, ее значение.
  10. Биологизаторские теории
  11. Биологическая обратная связь
  12. Биологическая обратная связь.

Обратная задача теории погрешности заключается в следующем: при каких значениях аргумента известная функция у=f(х1, х2,¼,хn) будет иметь погрешность не превосходящую заданной величины.

Простейшее решение обратной задачи дается принципом равных влияний. Согласно этому принципу предполагается, что все частные дифференциалы одинаково влияют на образование общей абсолютной погрешности.

Предельная погрешность функции у=f(х1, х2,¼,хn) для малых абсолютных погрешностей аргументов : .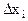

Оценка для относительной погрешности функции: или .

Пример: Найти предельные абсолютную и относительную погрешности объема шара , если d=3,7см±0,05 см; p»3,14.

Решение: Рассмотрим d и p как переменные величины. Вычислим частные производные , . При заданных значениях d и p получаем, что , .

Согласно правилу нахождения предельной абсолютной погрешности, имеем:

.

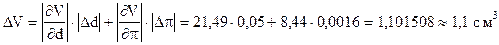Поэтому V»26,51±1,1 cм3. Относительная погрешность: .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)