Квадратурная формула Гаусса

Пусть функция y=f(x) задана на промежутке [-1,1]. Нужно подобрать узлы квадратурного правила и коэффициенты так, чтобы квадратурная формула

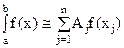(13)

была точной для всех полиномов f(x) наивысшей степени m=2n-1, т.к. имеем 2m неизвестных , а полином степени 2n-1 определяется 2n коэффициентами. Остаточный член обращается в нуль, когда , где С_i=const, i=0,¼,m. Тогда

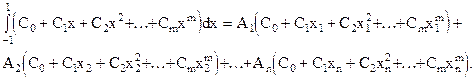
Учитывая соотношение: 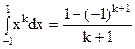, получаем систему 2n уравнений относительно :

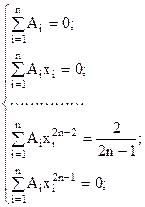(14)

Система (14) нелинейная, и её исследование громоздко. Поэтому воспользуемся теоремой:

для того чтобы квадратурная формула (13) интерполяционного типа была точна для всех многочленов степени не выше 2n-1, необходимо и достаточно, чтобы ее узлы x_j,были корнями многочлена w_n(x), ортогонального на [-1;1] к любому многочлену степени не выше n.

Ортогональную систему многочленов, имеющих n различных действительных корней на [-1;1], образуют многочлены Лежандра

(15)

Итак, в квадратурной формуле с n узлами, имеющей наивысшую степень точности 2n-1, узлы x_j,j=1,...,n являются корнями многочлена Лежандра n-ой степени, а из системы (14), зная x_j легко найдем А_j.

Для произвольного интервала[a,b] сделаем замену 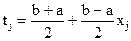. В этом случае формула Гаусса примет вид

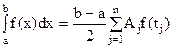. (16)

Таблица узлов и коэффициентов формулы Гаусса

Поиск по сайту: