Нахождение суммы

Задача 1. Пусть требуется вычислить сумму первых n натуральных чисел, т.е. . Задача сводится к организации арифметического цикла по i. Переменная цикла i будет выполнять две функции: номер очередного слагаемого и одновременно его значение.

Исходные данные: n - количество слагаемых (или значение последнего слагаемого). В цикле будет повторяться одно и то же действие: к предыдущему значению суммы прибавить очередное значение i (очередное слагаемое). Перед началом цикла необходимо обнулять значение переменной, в которой будет накапливаться сумма.

var S, i, n: integer; {S - сумма, i - слагаемое,

n - количество слагаемых}

begin

writeln (‘задайте количество слагаемых’);

readln (n);

S:= 0;

for i:= 1 to n do

S:= S + i;

writeln (‘cумма равна ‘, S)

end.

Эту же программу можно написать, используя операторы while и repeat.

Примечание: любую задачу, реализуемую с помощью арифметического цикла, можно запрограммировать, используя операторы while или repeat, но при этом необходимо не забывать об операторах, которые выделены чертой в приведенных выше программах.

Контрольный вопрос. Можно ли задачу, написанную с использованием операторов while или repeat, представить оператором for?

Задача 2. Найдите сумму n произвольных действительных чисел.

Эта задача отличается от предыдущей тем, что необходимо позаботиться о вводе слагаемых. В цикле будет вводиться очередное слагаемое и прибавляться к предыдущему значению суммы. Причем для различных слагаемых будет использоваться одна переменная, которая будет менять свое значение при выполнении каждого цикла. Таким образом будет введено n различных слагаемых. Достоинством такого ввода является экономия памяти, поскольку используется одна переменная, но по окончании цикла в данной переменной сохранится только последнее введенное значение, а все остальные будут утеряны.

var i, n: integer; {n - количество слагаемых, i - номер очередного

слагаемого}

S, a: real; {S - сумма, a - значение очередного слагаемого}

begin

writeln (‘задайте количество слагаемых’); readln (n);

S:= 0;

for i:= 1 to n do

begin write (‘введите очередное слагаемое’);

readln (a);

S:= S + a

end;

writeln (‘сумма =’, S)

end.

Задача 3. Организуйте вычисление суммы до тех пор, пока очередное слагаемое не станет равно нулю (или любому другому значению, которое выбирается в качестве барьера для вычислений).

var S, a: real;

i: integer;

begin

S:= 0; i:= 1;

writeln (‘введите первое слагаемое’);

readln (a);

while a <> 0 do

begin S:= S + a;

i:= i + 1;

write (‘введите’, i:2, ’-ое слагаемое’);

readln (a)

end;

writeln (‘сумма равна’, S)

end.

Циклическую часть можно оформить с помощью оператора repeat следующим образом:

i:= 0;

repeat

i:= i + 1;

write (‘введите’, i:2, ’-ое слагаемое’);

readln (a);

S:= S + a;

until a = 0;

Задача 4. Напишите программу вычисления суммы при заданном x:

.

В таких задачах для уменьшения общего количества выполняемых арифметических операций целесообразно следующее слагаемое вычислять, используя значение предыдущего слагаемого. При этом необходимо получить рекуррентную формулу, по которой будет вычисляться очередное слагаемое, для чего необходима дополнительная переменная.

Для данной суммы найдем рекуррентную зависимость i-го элемента от (i-1)-го.

.

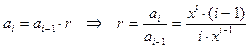
var y, x, ai: real;

n, i: integer;

begin

read (x, n);

ai:= x; y:= 0;

for i:= 2 to n+1 do

begin y:= y + ai;

ai:= ai * x * (i-1)/i

end;

writeln (‘y =‘, y);

end.

Внесем изменения в программу для того, чтобы она вычисляла сумму с заданной точностью, т.е. до тех пор, пока очередное слагаемое не станет меньше заданной точности. Эту задачу можно реализовать, используя итерационные циклы, поскольку неизвестно заранее, сколько слагаемых будет у суммы.

const eps = 0.001;

var y, x, ai: real;

n, i: integer;

begin

read (x, n);

ai:= x; y:= 0; i:= 1;

while abs (ai) >= eps do

begin y:= y + ai;

i:= i + 1;

ai:= ai * x * (i-1)/i

end;

writeln (‘y =‘, y);

end.

Задача 5. Найдите знакочередующуюся сумму: . Всего в этой сумме n слагаемых.

Нетрудно заметить, что нечетные элементы прибавляются, а четные - вычитаются.

Вариант 1. Будем отдельно вычислять сумму нечетных элементов и сумму четных элементов, а затем найдем их разность.

var i, n: integer; {i - значение очередного слагаемого:

n - количество слагаемых}

S1, S2: integer; {S1 - сумма нечетных элементов;

S2 - сумма четных элементов}

begin

write (‘задайте количество слагаемых’);

readln (n);

S1:= 0; S2:= 0;

i:= 1;

while i <= n do

begin S1:= S1 + i;

i:= i +2

end;

i:= 2;

while i <= n do

begin S2:= S2 + i;

i:= i +2

end;

writeln (‘сумма равна’, S1 - S2)

end.

Вариант 2. При вычислении суммы проверять: если элемент четный, то вычитать его из суммы, иначе - прибавлять.

var i, n: integer; {i - значение очередного слагаемого:

n - количество слагаемых}

S: integer; {S - сумма}

begin

write (‘задайте количество слагаемых’);

readln (n);

S:= 0;

for i:= 1 to n do

if i mod 2 = 0 then S:= S - i

else S:= S + i;

writeln (‘сумма равна ’, S)

end.

При вычислении следующей суммы можно заметить, что каждый второй элемент в тройке слагаемых вычитается. Это может быть представлено следующим образом:

S:= 0;

for i:= 1 to n do

if i mod 3 = 2 then S:= S - i

else S:= S + i;

Таким образом, можно сделать вывод, что j-ый элемент в группе из k элементов может быть определен следующим образом: i mod k = j.

Упражнения.

1. Найдите сумму: , где всего n слагаемых.

2. Вычислите:

а). Всего n слагаемых.

б). 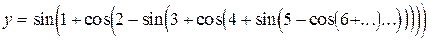. Всего n вложений функций.

3. Восстановите формулу, которая вычисляется программой:

Программа, рассмотренная выше, содержит цикл и разветвление. К этой же группе задач можно отнести задачи на нахождение количества и максимального (минимального) элемента.

Задача 6. Определите количество элементов в заданной последовательности вещественных чисел, которые являются четными, но имеют нечетные порядковые номера.

Для решения этой задачи необходимо организовать арифметический цикл по i и для каждого значения переменной проверять, удовлетворяет ли она заданному условию. Если условие выполняется, то к счетчику числа элементов прибавляется единица, иначе - переход к следующему значению числа.

var x: real; {значение очередного элемента}

i, n, k: integer; {i - номер очередного числа,

n - количество элементов,

k - счетчик}

begin

writeln (‘Задайте количество элементов’);

writeln (n);

k:= 0;

for i:= 1 to n do

begin write (‘введите очередное число’);

readln (x);

if (x mod 2 = 0) and (i mod 2 <> 0) then k:= k + 1

end;

writeln (‘ количество элементов ’, k)

end.

Задача 7. Найдите максимальный элемент в заданной последовательности целых чисел.

Предполагаем, что максимальным является первый элемент в заданной последовательности чисел. Затем в цикле проверяем не является ли очередной элемент больше кандидата на максимум, если да, то изменяем значение кандидата на максимум, в противном случае - переходим к следующему элементу.

var x: integer; {значение очередного элемента}

i, n, max: integer; {i - номер очередного числа,

n - количество элементов,

max - кандидат на максимум}

begin

writeln (‘ Задайте количество элементов’);

writeln (n);

writeln (‘ введите первое целое число’);

readln (max); {первое число - кандидат на максимум}

for i:= 2 to n do

begin write (‘ введите’, i:2, ‘число’);

readln (x);

if x > max then max:= x;

end;

writeln (‘ максимальный элемент равен ’, max)

end.

Задача 8. Найдите номер максимального элемента в данной последовательности.

Необходимо ввести дополнительную переменную, которая будет хранить порядковый номер кандидата на максимум. Программа будет выглядеть следующим образом.

var x: integer; {значение очередного элемента}

i, n, max, imax: integer; {i - номер очередного числа,

n - количество элементов,

max - кандидат на максимум imax - номер кандидата}

begin

writeln (‘ Задайте количество элементов’);

writeln (n);

writeln (‘ введите первое целое число’);

readln (max); {первое число - кандидат на максимум}

imax:= 1;

for i:= 2 to n do

begin write (‘ введите’, i:2, ‘число’);

readln (x);

if x > max then begin max:= x; imax:= i end;

end;

writeln (‘ максимальный элемент c номером’, imax, ‘равен ’, max)

end.

Задача 9. Дана последовательность чисел, в которой есть одинаковые числа. Найдите количество максимальных элементов.

Для решения этой задачи необходимо иметь переменную, которая будет накапливать количество максимальных элементов. Причем, при изменении значенияя кандидата на максимум необходимо начинать считать количество максимальных элементов заново.

var x: integer; {значение очередного элемента}

i, n, max, Smax: integer; {i - номер очередного числа,

n - количество элементов,

max - кандидат на максимум Smax - количество максимальных

элементов}

begin

writeln (‘ Задайте количество элементов’);

writeln (n);

writeln (‘ введите первое целое число’);

readln (max); {первое число - кандидат на максимум}

Smax:= 1;

for i:= 2 to n do

begin write (‘ введите’, i:2, ‘число’);

readln (x);

if x > max then begin max:= x; Smax:= 1 end;

if x = max then Smax:= Smax +1

end;

writeln (‘ количество максимальных элементов равно ‘, Smax)

end.

Задача 10. В 1228 году итальнский математик Фибоначчи сформулировал интересную задачу: “Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения”.

Эта задача приводит к последовательности чисел 1, 1, 2, 3, 5, 8, 13, 21, …, где каждый последующий член равен сумме двух предыдущих, за исключением первых двух членов. Таким образом, необходимо иметь три переменные: предпредыдущий, предыдущий и определяемый члены. После вычисления очередного члена необходимо опять иметь два предыдущих члена, но уже новых. Так для определения 5 необходимо иметь 2 и 3, а для определения 8 – уже 3 и 5, т.е. ноебходимо осуществлять сдвиг по вычисленным значениям.

{программа определяет n-ое число Фибоначчи}

var a, b, c: integer; {a - предпредыдущее, b - предыдущее, c - текущее}

i, n: integer;

begin

write (‘Задайте количество чисел Фибоначчи’);

readln (n);

if (n = 1) or (n = 2) then writeln (n:2, ‘-ое число Фибоначчи равно 1’)

else

begin a:= 1; b:= 1;

for i:= 3 to n do

begin

c:= a + b;

a:= b; b:= c

end;

writeln (n:2, ‘-ое число Фибоначчи равно ’, c)

end;

end.

Упражнение. Измените программу таким образом, чтобы она определяла сумму всех чисел Фибоначчи, не превосходящих заданного N.

Особый интерес представляют поисковые задачи. Такая задача может быть сформулирована следующим образом.

Задача 11. Найдите первый элемент в заданной последовательности, совпадающий с заданным.

Особенностью задач такого типа являются две причины выхода из цикла: 1) найден заданный элемент, необходимо прекратить поиск, 2) элемент не найден, но закончилась заданная последовательность чисел. Реализуются такие задачи с использованием логической переменной, которая меняет свое значение, если найден искомый элемент.

var a, x: integer; {a - очередное число, x - искомый элемент}

i, n: integer;

t: boolean;

begin

write (‘Задайте количество чисел в последовательности’);

readln (n);

write (‘искомый элемент’);

readln (x);

t:= false; {искомый элемент не найден}

i:= 1;

while (i <= n) and not t do {пока есть элементы и не найдено}

begin write (‘введите число из последовательности’);

readln (a);

if a = x then t:= true {нашли элемент}

else i:= i +1; {переход к следующему}

end;

if t then writeln (‘Нашли элемент с номером’, i)

else writeln (‘Такого элемента нет’);

end.

Упражнения.

1. Напишите программу, проверяющую является ли заданная последовательность вещественных чисел неубывающей. Примечание. Две причины выхода из цикла: 1) - нарушение условия не убывания и 2) просмотрены все элементы. Необходимо использовать логическую переменную. Кроме того, обработка идет по два элемента, а ввод - поэлементно, поэтому необходима дополнительная переменная, хранящая предыдущее число.

2. Найдите первую пару элементов в заданной последовательности вещественных чисел, которые принадлежат интервалу [a, b] и первые две цифры дробной части которых равны.

Поиск по сайту: