Нахождение вероятнейших координат места судна

Две линии положения всегда пересекаются в одной точке, поскольку решение системы уравнений двух линий положения в общем виде всегда приводит к однозначному определению неизвестных членов уравнений Dj и Dl.

Однако при такой обсервации невозможно обнаружить и оце­нить неизбежные погрешности наблюдений, ошибки вычислений и про­махи. Для получения более точного и надежного места необходимо выполнить дополнительные, или избыточные измерения навигационного параметра, по которым легко обнаружить промахи, оценить, исключить влияние систематических и уменьшить влияние случайных погрешностей линий положения.

Аналитически нахождение обсервованых координат места судна при на наличии избыточных линий положения заключается в решении системы уравнений вида:

а₁ Dj + b₁ Dl cosj = n₁;

a₂ Dj + b₂ Dl cosj = n₂;

...................;

а_i Dj + b_i Dl cosj = n_i.

где а_i= g_icosτ_i, b_i=g_isin τ_i – коэффициенты уравнений линий положения;

n_i=U_i – U_c – свободные члены уравнений линий положения (разница между измеренными и счислимыми значениями навигационного параметра).

Однако из-за неизбежных погрешностей измерения навигационных параметров свободные члены уравнений линий положения n_i отягощены случайными и систематическими погрешностями, тогда это уравнение иметь вид:

а₁ Dj + b₁ Dl cosj = n₁+υ₁;

a₂ Dj + b₂ Dl cosj = n₂+υ₂;

.....................;

а_i Dj + b_i Dl cosj = n_i+υ_i.

где υ_i - невязки, обусловленные наличием случайных и систематических погрешностей

Однако данная система уравнений является неопределенной, поскольку число неизвестных (Dj, Dl, и значений υ_i) больше числа уравнений системы.

При графическом решении задачи определения обсервованного места судна из-за неизбежных погрешностей измерения навигационных параметров, три, четыре и более линий положения в одной точке, как правило, не пересекаются, а образуют так называемую фигуру погрешностей. Задача состоит в том, чтобы отыскать вероятнейшее место судна в фигуре погрешностей и оценить его точность с учетом погрешностей линий положения.

Существуют различные вероятностные способы решения данной системы уравнений, однако в общем случае решение, как правило, осуществляется так называемым методом наименьших квадратов.

Сущность метода наименьших квадратов заключается в отыскании таких значений вероятнейших поправок к счислимым координатам Dj_в и Dl_в, при которых сумма квадратов невязок являлась бы величиной минимальной:

∑ υ_i²= [υυ] = min – для равноточных измерений;

или ∑p_i υ_i²= min– для неравноточных измерений,

где - вес навигационного параметра.

В данном случае предполагается, что погрешности измерений навигационного параметра подчинены нормальному закону распределения.

После ряда преобразований неопределенная система уравнений линий положения сводится к системе двух нормальных уравнений вида:

А₁Dj + В₁Dl cosj =L₁;

А₂Dj + В₂Dl cosj =L₂.

где А₁, В₁, А₂, В₂ – коэффициенты при неизвестных;

L₁, L₂ – свободные члены.

Аналитически решение данной системы уравнений выполняется либо методом определителей, либо методом итераций (методом Зейделя).

Решение по методу определителей заключается в вычислении коэффициентов при неизвестных А₁, В₁, А₂, В₂ и свободных членов L₁, L₂ уравнений.

Расчет вероятнейших поправок к счислимым координатам Dj_в и Dl_в при использовании метода определителей выполняется по формулам:

;

.

Вероятнейшие координаты места судна рассчитываются по формулам:

j_в=j_с + Dj_в;

l_в=l_с + Dl_в.

Решение по методу итераций (методу Зейделя ) заключается в последовательном вычислении поправок к счислимым координатам Dj_вi и Dl_вi и в сравнении их вычисленными ранее (на предыдущей итерации) поправками до тех пор, пока разница между i-ой и (i-1)-ой поправками будет менее некоторой заданной велиины.

Если количество измеренных навигационных параметров невелико (как правило, не более 3-х или 4-х), то задачу отыскания вероятнейшего места судна при обсервации с использованием избыточных линий положения можно решить и графически на морской навигационной карте, на планшете или на листе миллиметровой бумаги.

Существуют несколько графических способов отыскания вероятнейшего места судна в фигуре погрешностей. К ним относятся: способ весов (центрографический способ), способ противомедиан и способ биссектрис.

Если появление фигуры погрешностей обусловлено влиянием только случайных погрешностями измерений навигационного параметра, то вероятнейшее место будет всегда внутри фигуры погрешности. В данном случае для отыскания вероятнейшего места судна в фигуре погрешностей можно использовать способы весов (центрографический способ) и противомедиан.

Если в появлении фигуры погрешностей участвуют не только случайные, но и систематические погрешности измерений навигационного параметра, то для отыскания вероятнейшего места предпочтительнее использовать способ биссектрис.

Способ весов (центрографический способ)

Сущность данного способа (применительно к трегольнику погрешностей abc) заключается в следующем (рис. 8.1):

- рассчитываются градиенты навигационных параметров g_i и среднеквадратические погрешности линий положения:

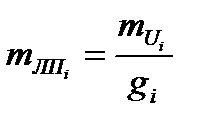
- вычисляются веса линий положения:

- вычисляются веса точек пересечения линий положения, т.е. вершин треугольника погрешности а, b, с:

;

;

.

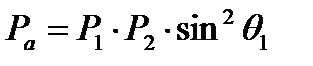пусть для примера Р_а=5, Р_b=3, а Р_с=1;

- одна из сторон тругольника abc делится на части, обратно пропорционльные весам соответствующих вершин. Так, если Р_b=3, а Р_с=1, то сторона bсделится на отрезки, пропорциональные 1: 3;

- полученной точке dприписывается вес, равный сумме весов вершин b и с, т.е. P_d = Р_b+ Р_с=1+3=4.

- полученная точка dсоединяется с третьей вершиной треугольника а, прямую adделится на отрезки, обратно пропорциональные весам точекa и d, то есть, в отношении 4: 5.

Рис 8.1 Нахождение вероятнейшего места судна в трегольнике погрешностей по способу весов (центрографическим способом)

Полученная точка Fна прямой adи будет вероятнейшим местом судна в треугольнике погрешности abc.

Рис. 8.2. Нахождение вероятнейшего места судна в четырехугольнике погрешностей по способу весов (центрографическим способом)

При определении места по четырем линиям положения необходимо стороны четырехугольника погрешности (рис. 8.2) азделить в отношениях, обратно пропорциональных весам прилегающих линий положения, тогда обсервованное место найдется в точке пересечения прямых, соединяющих попарно полученные точки.

Центрографический приём достаточно универсален и может быть применен при любом числе линий положения, однако не учитывает влияния систематических погрешностей измерения навигационного параметра.

Способ противомедиан

Если место судна определяется по трем равноточным (то есть имеющим равный вес) линиям положе­ния, то вероятнейшее место судна будет сов­падать с точкой пересечения противомедиан.

Противомедиана - это прямая, симметричная меди­ане относительно биссектрисы угла между ними (рис. 8.3)

Рис. 8.3 Нахождение вероятнейшего места судна способом противомедиан

Для построения противомедианы из вершины треугольника проводится медиана - прямая, делящая противоположную сторону пополам. Затем откладывается меньший угол от противоположной стороны угла треугольника.

Поскольку способ противомедиан предусматривает наличие в измерениях навигационного параметра только случайных погрешностей, то вероятнейшее место судна будет находится при любом расположении ориентиров всегда внутри фигуры погрешностей на пересечении противомедиан треугольника (рис.8.3).

Следует отметить, что, несмотря на то, что с математической точки зрения способ проивомедиан является наиболее строгим для отыскания вероятнейшего место судна в трегольнике погрешностей при наличии в линиях положения только погрешностей случайных, он достаточно трудоемок.

Поэтому на практике без особого ущерба на точность вероятнейшего места судна способ противомедиан часто заменяется более простым с точки зрения графических построений (но заведомо менее точным) способом биссектисс.

Способ биссектрис

Способ биссектрис из всех вышеперечисленных способов является наиболее простым и достаточно точным. Кроме того он, в отличие от способов весов и противомедиан, позволяет при определении вероятнейшего места судна учесть и влияние систематических погрешностей.

При использовании данного способа вероятнейшее место судна находится следующим образом:

Рис. 8.4. Нахождение вероятнейшего места судна способом биссекрисс при расположения навигационных ориентиров по всему горизонту

- если градиенты линий положения направлены по всему горизонту, то есть навигационные ориентиры рас­положены по всему горизонту, то вероятнейшее место всегда будет находиться внутри треугольника погрешностей на пересечении его биссектрис независимо от соотношения в измерениях случайных и систематических погрешностей (рис. 8.4).

- если градиенты линий положения направлены в одну половину горизонта, то есть навигационные ориентиры рас­положены по одну сторону горизонту, то вероятнейшее место судна находится следующим образом:

а. находится точка М_о1 внутри фигуры погрешностей на пересечении биссектрис внутренних углов треугольника (Рис. 8.5). По своей сути это точка - вероятнейшее места судна при условии, что в линиях положения имеются только случайные погреш­ности;

б. находится точка М_о2 вне фигуры погрешностей в стороне, противоположной направлениям градиентов на пересечении биссектрис одного внутреннего и двух смежных углов треугольника. По своей сути это точка - вероятнейшее места судна при условии, что в линиях положения имеются только систематические погреш­ности (Рис.8.5);

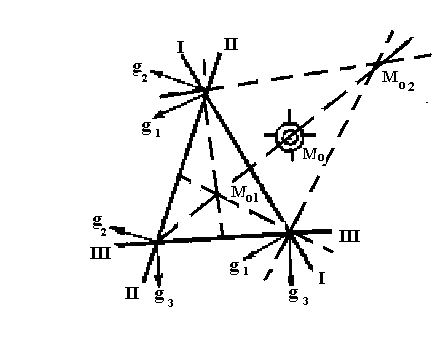
Рис. 8.5 Нахождение вероятнейшего места судна способом биссекрисс с учетом случайных и систематических погрешностей при расположении навигационных ориентиров по одну сторону горизонта

- находится вероятнейшее места судна - точка М_о на линии соединяющей точки М_о1 и М_о2, при этом отрезок М_о1М_о2 делится пропорционально соотношению случайных и систематических погрешностей. Если такое соотношение неизвестно, то предполагается, что проявление случайных и систематических погрешностей равновероятно, и тогда вероятнейшее место судна принимается на середине прямой, соединяющей точки М_о1 и М_о2 (рис. 8.5).

Оценка точности вероятнейшего места судна, полученного с использованием избыточных измерений навигационных параметров, так же как и обсервованного места судна, полученного по измерениям двух навигационных параметров, может быть выполнена либо эллипсом погрешностей, либо радиальной среднеквадратической погрешностью.

При аналитическом решении задачи определения вероятнейшего места судна, полученного с использованием избыточных измерений навигационных параметров, вычисление элементов эллипса погрешностей выполняется по формулам:

;

;

;

D=A₁B₂-A₂B₁.

Вычисление радиальной среднеквадратической погрешности вероятнейших координат места судна выполняется по формуле:

.

При использовании центрографического способа (способа весов) оценка точности может быть выполнена путем построения так называемого полигона весов с последующим расчетом размеров полуосей эллипса погрешностей.

Любое количество линий положения, соответсвующим измеренным навигационным параметрам, можно заменить двумя так называемыми эквивалентными линиями положения, пересекающими под прямым углом в точке, соответсвующей вероятнейшему месту судна. Эквивалентные линии положения параллельны большой и малой полуосям эллипса погрешностей.

Тогда оценка точности вероятнейшего места судна эллипсом погрешностей выполняется следующим образом:

- рассчитываются направления τ_i и величины g_i градиентов навигационных параметров;

- по формуле 4.41 вычисляются веса линий положения;

- вычисляется сумма весов эквивалентных линий положения, которая равна сумме всех весов всех исходных линий положения:

;

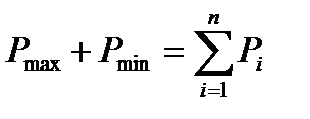где Р_max, Р_min - веса эквивалентных линий положения;

n - количество линий положения;

- строится полигон весов (рис. 8.6), для чего из произвольной точки А под углом, равным 2τ₁ относительно истинного меридиана прокладывается вектор, равный весу Р₁ первой линии положения, из его конца под углом 2 τ₂ прокладывается вектор, равный весу Р₂ второй линии положения и так далее. После чего измеряется длина замыкающего вектора полигона весов g, которая равна разности весов эквивалентных линий положения:

;

- измеряется угол 2Т, который составляет с истинным ме­ридианом замыкающий вектор полигона весов. Его поло­вина, то есть угол Т, представляет собой направление малой полуоси b эллипса погрешностей;

- находятся веса эквивалентных линий положения:

;

;

Рис. 8.6. Полигон весов

- вычисляются размеры полуосей эллипса погрешностей:

;

;

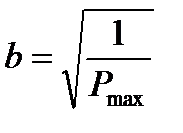Зная значения этих полуосей, можно рассчитать и радиальную среднеквадратическую погрешность вероятнейшего места судна по формуле:

.

Если необходимо оценить точность вероятнейшего места судна только радиальной среднеквадратической погрешностью без расчета элементов эллипса погрешностей, то можно воспользоваться следующей формулой:

.

При использовании для нахождения вероятнейшего места судна способа противомедиан или способа биссектрис в треугольнике погрешностей для независимых и равноточных измерений навигационного параметра расчет радиальной среднеквадратической погрешности может быть выполнен по формуле:

;

где: θ_1,2, θ_2,3, θ_1,3 - внутренние углы треугольника погрешностей.

Если разность азимутов ∆А близка к 120°, то есть треугольник близок к равнобедеренному, то без особого ущерба для точности данную формулу можно заменить более простой:

.

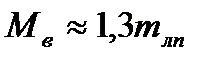При использовании для нахождения вероятнейшего места судна способа противомедиан или способа биссектрис в четырехугольнике погрешностей для независимых и равноточных измерений навигационного параметра расчет радиальной среднеквадратической погрешности может быть выполнен по формуле:

;

где γ - меньший из углов пересечения биссектрисс;

∆А_i - разность азимутов взаимно противоположных линий положения.

Если разность азимутов ∆А близка к 90°, то есть фигура погрешностей близка к прямоугольнику, то без особого ущерба для точности данную формулу можно заменить более простой:

.

Требования ИМО к точности места судна, оборудованного приемной аппаратурой глобальной навигационной спутниковой системы, регламентируются Резолюцией ИМО А.953 от 05.12.2003 г. Минимальные общие требования данной Резолюции в зависимости от района плавания по обеспечению навигационной безопасности судовождения приведены в Приложении 1.

Детализация требований данной Резолюции применительно к конкретным районам и морским операциям приведены в Приложении 2.

Поиск по сайту: