Форма и размеры Земли

1. Какие альтернативы развития открылись перед страной в марте 1953 г.?

2. Какие изменения в государственном строительстве и в стране в целом произошли в 1953-1964 гг.?

3. Какие примеры свидетельствуют о непоследовательности и ограниченности политических преобразований, начатых Н.С.Хрущёвым?

4. Какие попытки реорганизации экономической жизни страны предпринимались в 50-е - начале 60-х гг.?

5. Какие достижения СССР в освоении космоса и в других научно-технических сферах вы знаете?

6. В чём вы видите особенности общественно-политического развития СССР в период с середины 60-х до середины 80-х гг.?

7. Определите основные идеи и принципы экономической реформы 1965 г.

8. В чём состоит главная причина того, что советское руководство и лидеры западных стран пошли в первой половине 70-х гг. на разрядку международной напряжённости?

9. Почему Советский Союз ввёл свои войска в Афганистан в 1979 г.?

10. Какого рода проблемы и трудности проявились в стране в 80-егг.?

11. Основные направления внешней политики СССР в 60-80-е гг. XX в.

12. Раскройте роль таких международных организаций, как ВТО и МВФ, в мировом экономическом развитии.

13. Объясните, какую роль в национальных экономиках отдельных
стран играют транснациональные производственные комплексы.

Форма и размеры Земли

Физическая поверхность Земли образуется поверхностью океанов и рельефом материков и островов. Уровенной поверхностью называется такая форма Земли, которая образуется поверхностью Мирового океана, мысленно продолженной над материками и островами. (Ри.1.1). Такая фигура имеет неправильную форму, не совпадающую в точности с формой ни одного из известных геометрических тел и называется геоидом. Неправильность формы геоида обусловлена неравномерным распределением плотности масс в толще Земли. Поверхность геоида во всех точках перпендикулярна направлению силы тяжести в этих точ­ках.

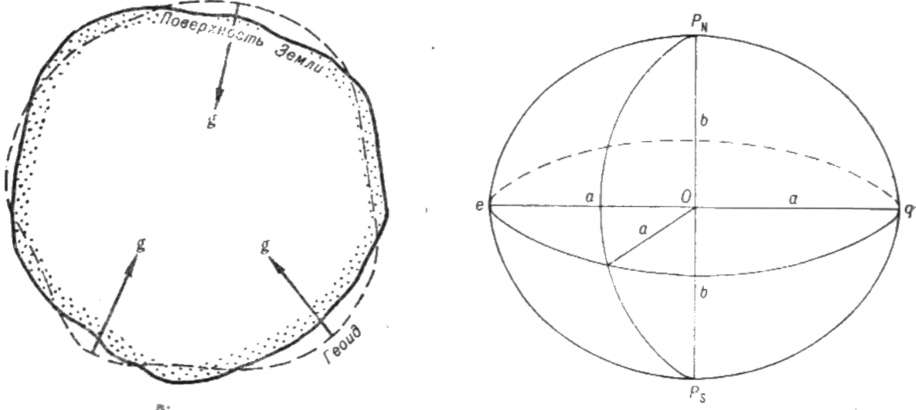
Рис.1.1 Форма Земли.

При решении задач судовождения, связанных с обработкой ре­зультатов измерений, выполненных на земной поверхности, сложную фигуру геоида заменяют более простой правильной фигурой, поддаю­щейся математическому описанию. Такой фигурой является эллипсоид (сфероид) - фигура, образованная вращением эллипса вокруг его ма­лой оси. Эллипсоид, моделирующий Землю, называют земным эллипсоидом.

Основными элементами земного эллипсоида являются размеры его большойи малой полуосей - величины а и b (рис. 1.2) или большая полуось а и полярное сжатие (относительная разность длин главных полуосей) a = (а -b)/а. Иногда сжатия a применяется другая характеристика — эксцентриситет эллипсоида .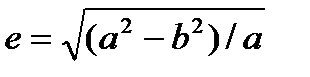

Из-за различия фигур геоида и эллипсоида невозможно добиться полного совпадения всех точек их поверхностей. Даже при самом опти­мальном подборе размеров и способа ориентировки земного эллип­соида его поверхность на отдельных участках может отстоять по высоте от поверхности геоида на несколько десятков метров. В разных странах за фигуру Земли принимают такие земные эллипсоиды, по­верхности которых наиболее близко совпадают с поверхностью геоида на территории данной страны.

Земной эллипсоид определенных размеров, принятый в данном государстве за фигуру Земли, называют референц-эллипсоидом.

Рис. 1.2Земной эллипсоид.

В нашей стране с 1946 г. в качестве референц-эллипсоида при­нят эллипсоид Ф. Н. Красовского со следующими элементами:

-большая полуось а=6378245 м;

-малая полуось =6 356 863 м;

-полярное сжатие a = 1/298,3= 0,003 352 330.

Поверхность эллипсоида Красовского совмещена с поверхностью геоида в исходной точке, за которую принят центр Круглого зала Пул­ковской обсерватории. При этом за исходный уровень поверхностей принят нуль Кронштадтского футштока. Отклонение референц-эллипсоида Красовского от соответствующих точек на поверхности геоида не превышает 150 м.

Для согласования результатов измерений на земной поверхности, производимых в различных государствах, рассчитываются общеземные, или международные референц-эллипсоиды, оптимальные по критерию минимума отклонения от поверхности геоида в целом. Такие модели международных референц-эллипсоидов приняты в системах спутниковой навигации. Так в СНС ГЛОНАСС в качестве опорного принят референц-эллипсоид ПЗ-90(SGS-90) –это несколько уточненный по данным наблюдений из космоса эллипсоид Красовского, а в СНС GPS - референц-эллипсоид WGS-84.

Для определения положения судна на земной поверхности и на­правления его движения используются следующие условные точки, линии и плоскости (рис. 1.3):

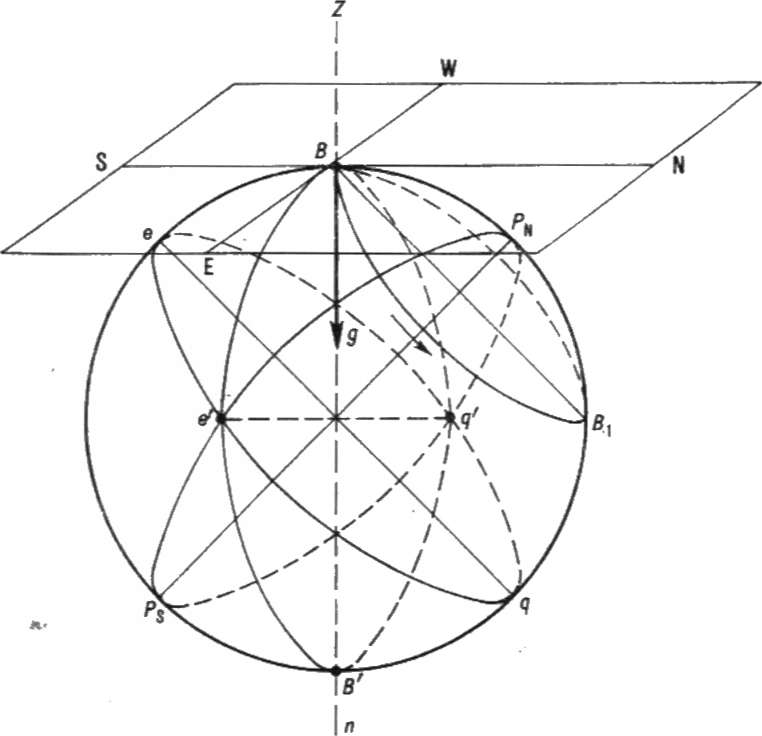
Рис. 1.3 Основные точки, линии и плоскости на земной поверхности.

Земная ось-прямая Р_NР_S, вокруг которой происходит суточное вращение Земли. Эта ось совпадает с малой осью земного эллипсоида.

Географические полюса Земли Р_N и Р_S - точки пересечения земной оси с поверхностью Земли. Полюс Р_N, со стороны которого вращение Земли усматривается против направления движения часовой стрелки, называется северным, противоположный полюс Р_S - южным.

Параллели- линии, образованные пересечением плоскостей, пер­пендикулярных земной оси, с поверхностью земного эллипсоида (на­пример, линия ВВ₁).

Экватор - параллель eq, плоскость которой проходит через центр Земли (наибольшая по длине параллель).

Меридианы истинные, или географические, - линии, образованные пересечением плоскостей, проходящих через земную ось, с поверх­ностью земного эллипсоида (например, линии Р_NеР_Sq, Р_Nе¢Р_Sq¢ и т. п.). Эти плоскости называются плоскостями истинных, или географических, меридианов.

Меридиан наблюдателя (местный меридиан) - меридиан, проходя­щий через место наблюдателя (заданное место). Если, например, на­блюдатель находится в точке В, то меридианом этого наблюдателя, является линия Р_NВР_S В¢.

Вертикальная, или отвесная, линия - прямая ZBB'n, совпадающая с направлением силы тяжести g в данной точке.

Зенит наблюдателя - точка Z пересечения отвесной линии с вооб­ражаемой небесной сферой. Противоположная точка n называется на­диром.

Плоскость истинного горизонта наблюдателя - горизонтальная плоскость, проходящая через место наблюдателя перпендикулярно отвесной линии.

Полуденная линия - линия NS, образованная пересечением пло­скости меридиана наблюдателя с плоскостью истинного горизонта. Эта линия соответствует направлениям из места наблюдателя на север и на юг. Направление от В к N — северная часть истинного меридиана, а направление от В к S — южная часть этого меридиана.

Вертикальные плоскости - плоскости, проходящие через отвесную линию.

Плоскость первого вертикала - вертикальная плоскость, перпенди­кулярная плоскости меридиана наблюдателя.

Линия восток - запад (Е - W) - линия пересечения плоскости пер­вого вертикала с плоскостью истинного горизонта наблюдателя.

Линии N - S и Е - W означают главные направления (румбы).

Положение судна на земной поверхности опре­деляется двумя координатами. Существует несколько систем координат, основными из которых в судовождении являются географическая, квазигеографическая, прямоугольная и полярная.

Географическая система является основной системой координат, используемой в судовождении. Координатными осями в этой системевляются экватор и начальный меридиан — меридиан Гринвичской обсерватории (Англия). Координатными линиями являются параллели и меридианы, а координатами - широта и долгота.

Географической широтой j точки называется угол между нормалью к поверхности Земли в этой точке и плоскостью экватора (рис. 1.4. 1.5, 1.6). Географическая широта измеряется дугой меридиана от экватора до данной точки от 0 до 90°, ей приписывается наименование N (знак плюс) или S (знак минус).

Геоцентрической широтой φ' называется угол между плоскостью экватора и прямой, соединяющей центр сфероида с данной точкой, т. е. φ'=LqOT (рис. 1.5).

Приведённая широта u есть угол между плоскостью экватора и радиусом ОТ₁, проведённым из центра из центра сферы в точку Т₁ (рис. 1.6).

Между географической и геоцентрической широтами существует следующая зависимость:

φ'= φ-11,5'sin2φ.

Географическая и приведённая широты связаны следующей формулой:

u=φ-5,8'sin2φ.

Разностью широт ∆φ называется дуга меридиана между параллелями пункта прихода φ₂и пункта отхода φ₁(рис. 1.7):

∆φ=φ₂- φ₁

Разность широт измеряется в пределах от 0 до 180° и имеет наименование к N или к S. При математических вычислениях вместо наименования используются знаки (+) или (-) соответственно.

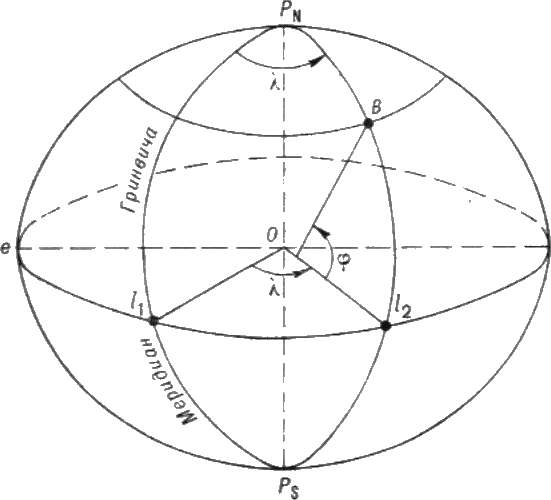
Рис. 1.4 Географическая система координат

Рис. 1.5. Географическая и геоцентрическая широта.

Географической долготой l точки называется двугранный угол между плоскостью гринвичского меридиана и плоскостью меридиана данной точки. Долгота измеряется дугой экватора от начального (гринвичского) меридиана до меридиана данной точки.

Счет долготы ведется к востоку и западу от гринвичского меридиана от 0° до 180°. Долготы точек восточного полушария имеют наименование Е (восточная), при вычислениях им приписывается знак плюс. Долготы точек западного полушария имеют наименование W (западная), при вычислениях им приписывается знак минус.

Разностью долгот ∆λ называется наименьшая из дуг экватора между меридианами пункта прихода λ₂ и пункта отхода λ₁ (рис. 1.8):

∆λ=λ₂- λ₁

Разность долгот измеряется в пределах от 0 до 180° и имеет наименование к Е или к W. При вычислениях вместо наименования используются знаки (+) или (-) соответственно. Если разность долгот будет больше 180° (∆λ'>180°), то её вычитают из 360°, т. е.

∆λ=360°- ∆λ'

Рис. 1.6. Географическая и приведённая широта.

Рис. 1.7 Разность широт

В этом случае наименование (знак) разности долгот следует сменить на противоположный.

Ортодромией называется кратчайшее расстояние между двумя точками на поверхности сферы. Она измеряется по меньшей дуге большого круга, образованного пересечением плоскости проходящей через центр сферы и заданные точки, со сферической поверхностью.

Основные свойства ортодромии:

- она является дугой большого круга и служит кратчайшим расстоянием между двумя точками на поверхности сферы;

- через две точки на поверхности сферы Т₁(φ₁, λ₁) и Т₂(φ₂, λ₂)можно провести только одну ортодромию (рис. 1.9);

- ортодромия пересекает разные меридианы под разными углами, то есть А₁≠ А₂.

Рис. 1.8. Разность долгот.

Рис. 1.9. Ортодромия и локсодромия.

Локсодромией называется линия на поверхности Земли, которая пересекает все меридианы под одним и тем же углом. Локсодромия не является кратчайшим расстоянием между двумя точками на поверхности Земли. Однако плавание локсодромическим курсом имеет большие удобства и с появлением компаса является основой морской навигации.

В общем случае локсодромия и ортодромия имеют различную кривизну, т.е. локсодромия и ортодромия в данной точке пересекаются под некоторым углом (рис. 1.10). Угол между локсодромией и ортодромией в данной точке называется ортодромической поправкой ψ. На сравнительно небольших расстояниях (500-600 миль) эту поправку вычисляют по формуле:

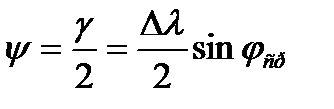
Ортодромическая поправка служит для перевода ортодромических направлений (курсов, пеленгов) в локсодромическое по формуле:

К_лок=К_орт+ψ;

П_лок=А+ψ

Ортодромическую поправку можно выбрать из таблицы 2.12 МТ-2000 или из таблицы. 23-а (по φ_ср и Dλ при Dλ ≤5°)и по табл. 23-б МТ-75 по (φ₁, φ₂ и Dλ - в остальных случаях). Ортодромическая поправка может быть положительной и отрицательной.

Знак ортодромической поправки определяется по правилу:

- в северной широте ортодромическая поправка имеет знак (+), если ортодромическое направление меньше 180°, и знак (-), если ортодромическое направление больше 180°;

- в южной широте ортодромическая поправка имеет знак (+), если ортодромическое направление больше 180°, и знак (-), если ортодромическое направление меньше 180°.

Рис. 1.10. Ортодромическая поправка.

Поиск по сайту: