Погрешности измерений

Измерением называется физический процесс сравнения измеряемой величины с единицей измерения (эталоном). Однократное измерение данной навига­ционной величины называют наблюдением.

Измерение производится с помощью приборов или инструментов. В процессе измерения участвует также оператор, производящий измерения, объект измерения и внешняя среда.

Измерения навигационных элементов, а, следовательно, и навигационная информация в целом, классифицируются по нескольким признакам.

- по виду измерений: прямые (непосредственные) и кос­венные;

- по относительной точности: равноточные и неравноточные;

- по составу: однородные и разнородные;

- по степени полноты: необхо­димые и избыточные;

- по степени взаимозависимости: независимые и взаимозависимые;

- по характеру измерений: дискретные и непрерыв­ные.

Погрешностью измерения называется разница между измеренным и истинным значениями навигационного элемента.

Непосредственными источниками возникновения погрешностей измерений являются:

- несовершенство измерительных приборов;

- несовершенство органов чувств человека и нестабильность его состояния в процессе измерения;

- нестабильность параметров окружающей среды.

Абсолютнойпогрешностью навигационного элемента ∆ называется разность между измеренным U и истинным U_o значениями навигационного элемента, выраженная в единицах измеряемой величины:

∆ = U – U_o.

Однако на практике абсолютная погрешность бывает, как правило, неизвестна, так как неизвестна истинное значение навигационного элемента U_o.

Относительной погрешностью ∆_отн называется безразмерная величина, равная отношению абсолютной погрешности к измеренной величине навигационного элемента:

.

Абсолютная погрешность имеет размерность самого навигационного элемента, а относительная погрешность выражается отвлеченным числом (дробью) или в процентах.

Все погрешности по своим свойствам и характеру воздействия на результат подразделяются на систематические, случайные и грубые (промахи).

К систематическим погрешностям относятся такие погрешности, которые остаются постоянными или закономерно изменяющимися для всех навигационных измерений рассматриваемой совокупности. Систематические погрешности являются следствием неучтенного постоянного или закономерно изменяющегося воздействия факторов. Важнейшим свойством систематических погрешностей является их определенность по величине и знаку. Систематические погрешности чаще всего функционально связаны с методами, условиями и средствами измерений. Систематические погрешности могут и должны быть определены и исключены из результатов всех измерений. Этого можно достичь введением поправок, выверкой приборов и применением более рациональной методики измерений.

Поправкой измерительного прибора называется его систематическая погрешность, взятая с обратным знаком.

Случайнымисчитаются такие погрешности, величина и знак которых изменяются от измерений к измерению одной и той же величины в данных условиях. Эти погрешности появляются в результате совместного действия большого числа разнообразных факторов. При этом каждый фактор проявляется случайно. При выполнении серии измерений одного и того же навигационного параметра получают некоторую совокупность случайных погрешностей. Эта совокупность погрешностей обнаруживает определенную закономерность. Математические выражения такой закономерности определяет закон распределения случайных погрешностей. Зная закон распределения случайных погрешностей, можно определить вероятность появления случайных погрешностей и их численные характеристики (математическое ожидание, дисперсию, среднеквадратическую погрешность

Применительно к измерениям навигационных элементов, а в особенности навигационных параметров, случайные погрешности по характеру их проявления можно подразделить на частные и общие (повторяющейся).

Частной случайной погрешностью называется случайная погрешность, возникающая только за счет влияния непосредственно условий измерений - случайных погрешностей измерительных приборов, погрешностей органов чувств человека, влияния параметров окружающей среды.

Общей (повторяющейся) случайной погрешностью называется случайная погрешность определения поправки прибора характеризующая точность определения этой поправки. Характер проявления этой погрешности состоит в следующем.

Влияние систематической погрешности на измерение устраняется путем учета поправки, равной по величине и противоположной по знаку значению систематической погрешности. Определение такой поправки в большинстве случаев выполняется по ограниченному числу наблюдений, где статистической оценкой истинного значения случайной величины служит значение математического ожидания (среднего арифметического) случайной величины. Поэтому полной компенсации случайных погрешностей при определении поправки не происходит и сама систематическая погрешность (поправка) будет содержать погрешность случайную.

Таким образом величина (общей) повторяющейся случайной погрешности является статистической оценкой точности определения систематической погрешности (поправки) определенной при ограниченном количестве наблюдений.

Таким образом после введения поправок, компенсирующих систематическую погрешность измерительного прибора полная случайная погрешность будет состоять из двух составляющих:

- из частной случайной погрешности измерения;

- из общей (повторяющейся) случайной погрешности определения поправки (равной по величине и обратной по знаку систематической погрешности) измерительного прибора, характеризующей точность определения этой поправки.

Зависимость между частными m_ч и повторяющимися m_о погрешностями носит не функциональный, а вероятностный характер. Такая зависимость называется корреляционной. Корреляционная зависимость проявляется статистическими методами, так как эта взаимосвязь завуалирована влиянием многих случайных факторов.

Степень корреляционной зависимости двух измерений характеризуется безразмерной величиной, называемой коэффициентом корреляции r, который можно вычислить по формуле:

,

где m_о - СКП повторяющихся (общих) случайных погрешностей;

m_пi – полные СКП случайных погрешностей.

Для равноточных взаимозависимых измерений, то есть для измерений с m_п1=m_п2 коэффициентом корреляции r рассчитывается как:

.

Коэффициент корреляции изменяется в пределах от 0 до. Если r = 0, то есть m_о=0, то измеренные навигационные параметры считаются полностью независимыми, если r = 1, то измеренные навигационные параметры считаются полностью взаимозависимыми.

Среднеквадратической погрешностью ( СКП) случайной величины m(Х) называется статистическая оценка стандарта при ограниченном количестве n;

m(Х)=σ(Х)= 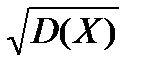при n®¥.

Для нормального закона распределения вероятность нахождения случайной величины в пределах М(X)±m(Х) составляет 68,3%.

Предельной погрешностью 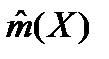называется такая погрешность, вероятность появления которой в данном ряду измерений ничтожно мала.

Для нормального закона распределения вероятность появления погрешности, равной 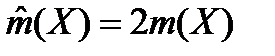составляет 1-0,95=0,05, а вероятность появления погрешности, равной составляет 1-0,997=0,003.

К грубым погрешностям или промахам относятся такие погрешности, численные значения которых выходят за пределы, допустимые для данного рода измерений или вычислений. Основными причинами их появления являются в большинстве случаев невнимательность и неопытность, а также халатность наблюдателя. Грубые погрешности заранее учесть невозможно, но их можно предупредить путем тщательного контроля измерений и обработки этих измерений. Измерения, которые содержат грубые погрешности, должны быть исключены из серии наблюдений.

Для нормального закона распределения с вероятностью 0,95 промахами будут считаться измерения, выходящие за пределы М(Х)±2m(Х), а с вероятностью 0,997 - выходящие за пределы М(Х)±3m(Х).

Поиск по сайту: