Погрешности прямых измерений физических величин

Изложение вопроса уместно начать с определения истинного и действительного значений физической величины и погрешности измерений, рассмотренных нами в первой главе.

Истинное значение физической величины – такое значение физической величины, которое идеальным образом характеризует в качественном и количественном отношениях соответствующую физическую величину. Ее обычно обозначают символом Х _ист.

Действительное (или измеренное) значение физической величины – значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него. Ее принято обозначать символом Х _изм.

Погрешность – отклонение результатов измерения от истинного значения измеряемой величины – обозначают символом Х (иногда Х_изм). Следовательно, Х = Х _ист- Х _изм.

Величина погрешности может быть выражена в тех же единицах измерения, что Х _ист и Х _изм:

[ Х ] = [ Х _ист] = [ Х _изм].

В этом случае ее называют абсолютной погрешностью.

Абсолютную погрешность, отнесенную к истинному или измеренному значению величины, называют относительной погрешностью и обозначают символом . Выражают в долях от единицы или в процентах. Например:

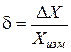либо

Погрешность – сложная величина, в общем виде она содержит следующие составляющие:

методическую погрешность, возникающую из-за несовершенства метода измерения, как правило, из-за ограниченной точности формул
и т. д.;

инструментальную погрешность, обусловленную неточностью применяемого измерительного устройства;

погрешности считывания и квантования, из них первые возникают из-за субъективных особенностей оператора, выполняющего измерения, а вторые – в цифровых приборах и дискретных преобразователях;

погрешности обработки данных наблюдений (измерений).

Некоторые из перечисленных погрешностей возникают случайно, например, при считывании показаний приборов, другие повторяются систематически (методическая и инструментальная погрешности) или изменяются по определенному закону. Следовательно, погрешности могут быть случайными и систематическими.

Наконец, следует выделить промахи – грубые ошибки, вызываемые неправильными действиями оператора или внезапным отказом прибора. В результат измерения их не засчитывают.

Структура погрешности измерения может быть разной, но наиболее распространенной является та, при которой полная (или суммарная) погрешность Х одновременно учитывает случайную погрешность измерения Х _сл и систематическую (приборную) погрешность измерения Х _сист.

Вызвано это тем, что они наиболее значимы по величине, а другие погрешности не существенны и ими пренебрегают.

Систематическая погрешность измерения Х _сист состоит, в основном, из приборной погрешности и она заранее известна (приведена
в паспорте на прибор или указана на самом приборе).

Случайная погрешность измерения Х _сл заранее не может быть определена, о появлении и величине ее можно утверждать лишь с некоторой степенью уверенности, называемой доверительной вероятностью Р.

При выполнении конкретных расчетов букву Х заменяют на символ, присвоенный физической величине. Например, если измеряют диаметр, то вместо Х пишут d или D. При измерении длины Х заменяют на L или l и т. д.

Косвенные измерения могут быть осуществлены, если некоторая часть физических величин (на которых они базируются) все-таки будет определена методом прямых измерений. По этой причине, в первую очередь, будет рассмотрен метод оценки погрешности прямых измерений.

В главе поставлены и раскрыты два вопроса:

1. Сведения из теории вероятностей о характере распределения измеряемых величин.

2. Алгоритм оценки погрешностей прямых измерений физических величин.

Поиск по сайту: