 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Сведения из теории вероятностей о характере распределения измеряемых величин
Вероятностькакого-либо события приблизительно равна частоте f (x) появления его и может быть рассчитана по зависимости:
 ,
,
где m – количество появлений наблюдаемого события; п – число проведенных опытов.
Например, если из 100 выстрелов в цель попало 37 пуль, то
f(x) =  = 0,37.
= 0,37.
Количество опытов п (в приведенном примере – количество выполненных выстрелов), при которых наблюдают событие m (попадание пули в мишень), должно быть достаточно большим. Только в этом случае можно будет судить о стабильности свойств этого и любого другого изучаемого явления, носящего вероятностный характер.
На основании этого допущения предполагают, что и при выполнении одного единственного выстрела численное значение f (x) = 0,37 сохранится.
Рассмотрим случай нескольких измерений n какой-либо физической величины Х, например, массы. При этом окажется, что ряд результатов совпадут друг с другом или будут очень близкими.
Если величину частоты f (x) появления некоторой величины Х  обозначить отрезком по оси ординат, то график можно представить следующим образом (рис. 1), где
обозначить отрезком по оси ординат, то график можно представить следующим образом (рис. 1), где  – центр распределения.
– центр распределения.

Рис. 1. Распределение частоты f (x) появления отдельных событий Х i
При большом числе наблюдений ( ) весь диапазон значений Х можно разбить на бесконечно малые интервалы dx и тогда данные рис. 1 предстанут в виде некоторой плавной кривой (рис. 2). Ее называют плотностью вероятности или нормальным законом распределения (распределение Гаусса) некоторой случайной величины Х.
) весь диапазон значений Х можно разбить на бесконечно малые интервалы dx и тогда данные рис. 1 предстанут в виде некоторой плавной кривой (рис. 2). Ее называют плотностью вероятности или нормальным законом распределения (распределение Гаусса) некоторой случайной величины Х.

Рис. 2. Распределение нормальное случайной величины Х
Разницу предельных значений  называют размахом результатов измерений. Рассеяние обусловлено обычно проявлением случайных причин при измерении и носит вероятностный характер.
называют размахом результатов измерений. Рассеяние обусловлено обычно проявлением случайных причин при измерении и носит вероятностный характер.
Разницу значений отклонений от среднего  и
и 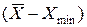 , называют рассеянием случайной величины Х. Для характеристики рассеяния служит основное отклонение, обозначаемое буквой
, называют рассеянием случайной величины Х. Для характеристики рассеяния служит основное отклонение, обозначаемое буквой  и рассчитываемое по уравнению:
и рассчитываемое по уравнению:

Из него видно, чем больше число измерений n, тем рассеяние меньше, и, следовательно, результат более точный.
Аналитически нормальное распределение описывают зависимостью:

Графическая интерпретация сущности этой зависимости представлена на рис. 3. Площадь под нормальной кривой, заключенная внутри промежутка от среднего значения до соответствующего количества основного отклонения (
 ,
,  2
2  ,
,  3
3  ,
,  4
4  ), численно равна вероятности Р того факта, что действительное значение отклонения от среднего значения будет содержаться внутри указанных интервалов.
), численно равна вероятности Р того факта, что действительное значение отклонения от среднего значения будет содержаться внутри указанных интервалов.

Рис. 3. Вероятность попадания измерений в заданный доверительный интервал
Теория вероятностей и накопленный опыт измерений показывают, что максимальные значения разницы  и
и  численно не превышают четырех основных отклонений 4
численно не превышают четырех основных отклонений 4  .
.
В этом случае численное значение вероятности Р тогофакта, что случайная величина Х будет находиться в заданном интервале, равно:



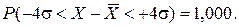
Принято вероятность Р называть доверительной вероятностью, что означает гарантию попадания отдельного результата измерения в заданный интервал.
Из приведенных формул видно, что значения случайной величины  , отклоняющиеся в обе стороны от среднего значения
, отклоняющиеся в обе стороны от среднего значения  не более, чем на величину основного отклонения
не более, чем на величину основного отклонения  , могут встретиться в 683 случаях на 1000 измерений. Аналогично для 2
, могут встретиться в 683 случаях на 1000 измерений. Аналогично для 2  – это составит 954 случая, для 3
– это составит 954 случая, для 3  – 997 случаев.
– 997 случаев.
Эти данные показывают, что хотя значения случайной величины могут изменяться неограниченно, в действительности (рис. 2.3) они укладываются в утроенное значение основного отклонения ( 3
3  ).
).
Выполнение большого количества измерений связано со значительными трудозатратами и поэтому неэкономично. В связи с этим интерес представляет получение достаточно достоверных, гарантированных с заданной доверительной вероятностью Р, иточных результатов при минимуме экспериментального материала.
Эту задачу решают на основе распределения Стьюдента. Сущность его состоит в том, что при переходе от  к достаточно малому их числу n = 2, …, 10, доля больших погрешностей возрастает, а доля малых уменьшается.
к достаточно малому их числу n = 2, …, 10, доля больших погрешностей возрастает, а доля малых уменьшается.
Последнее обстоятельство хорошо видно из сравнения распределений Гаусса и Стьюдента, представленных на рис. 4.
В силу отмеченных обстоятельств на практике используют распределение Стьюдента. Хотя сразу же необходимо заметить, что при 20-25 измерениях это распределение дает почти такие же результаты, что и нормальное распределение (распределение Гаусса).

Рис. 4. Графическая интерпретация распределений Гаусса и Стьюдента
В этом случае (как компенсацию меньшего числа проведенных опытов) вместо основного отклонения  для его оценки применяют величину средней квадратической погрешности результата измерения среднего арифметического значения
для его оценки применяют величину средней квадратической погрешности результата измерения среднего арифметического значения  (ранее ее называли стандартным отклонением):
(ранее ее называли стандартным отклонением):

В отличие от нормального распределения, где величину отклонения принимают кратной целому числу  (
(
 ,
,  2
2  ,
,  3
3  ,
,  4
4  ), в распределении Стьюдента вместо этих чисел применяют коэффициент
), в распределении Стьюдента вместо этих чисел применяют коэффициент  . Иногда его называют коэффициентом (статистикой) Стьюдента.
. Иногда его называют коэффициентом (статистикой) Стьюдента.
Нижние индексы у символа коэффициента  означают, что его значение зависит от величины требуемой доверительной вероятности результатов измерения Р и количества выполняемых опытов n.
означают, что его значение зависит от величины требуемой доверительной вероятности результатов измерения Р и количества выполняемых опытов n.
Численные значения  принимают из специальных таблиц
принимают из специальных таблиц
(приложение 3) в зависимости от принятых значений Р и n.
Величину доверительной вероятности принимают не менее 0,95 (ибо всякое событие, вероятность которого менее этой величины, считают мало достоверным). С другой стороны, большее ее значение (Р= 0,99; 0,999 и т. д.) должно быть заранее обосновано, исходя из важности социальной или экономической значимости выполняемых измерений.
Некоторое представление об этой операции можно получить из следующей таблицы:
Значения коэффициента Стьюдента
| Количество измерений п | Требуемое значение доверительной вероятности Р | ||
| Численные значения коэффициента Стьюдента | |||
| 0,95 | 0,99 | 0,999 | |
| 4,3 2,8 2,3 2,0 | 9,9 4,6 3,3 2,6 | 31,6 8,6 4,8 3,4 |
Тогда доверительный интервал, соответствующий принятой величине доверительной вероятности, будет равен:

Таким образом, коэффициент Стьюдента  увеличивает величину случайной ошибки, возникающей за счет уменьшения числа измерений.
увеличивает величину случайной ошибки, возникающей за счет уменьшения числа измерений.
В этом случае считают, что истинное значение измеряемой величины (без учета систематической погрешности технического средства измерения) будет находиться в интервале:

С учетом систематической погрешности технического средства измерения  результат измерения будет следующим:
результат измерения будет следующим:

Поиск по сайту: