 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Нахождение вероятнейших координат места судна. Очень часто в практике судовождения возникает ситуации, когда в районе плавания в достаточно короткий промежуток времени имеется возможность определить
Очень часто в практике судовождения возникает ситуации, когда в районе плавания в достаточно короткий промежуток времени имеется возможность определить обсервованные координаты места судна не одним, а несколькими способами. Это позволяет определить вероятнейшее место судна с большей точностью, чем точность каждой отдельной обсервации.
Обсервованные места на карту и сначала приводятся к одному моменту. Дня этого от каждой точки по направлению пути откладывается расстояние, проходимое судном за время между моментом обсервации и тем моментом, к которому она приводится. В дальнейшем определение вероятнейшего места судна выполняется так, как будто все они выполнены одновременно. Такое определение координат вероятнейшего места судна практике судовождения получил название метода осреднения мест.
Осреднение мест и расчет координат вероятнейшего места можно произвести аналитически и графически.
В обоих случаях сначала необходимо рассчитать, веса всех обсерваций. Вес обсервации Роi принимается обратным квадрату среднеквадратической погрешности обсервации Моi:

Счислимое место судна также несет в себе определенную навигационную информации, поэтому пренебрегать такой информацией не следует. Если при анализе полученных при обсервациях невязок Сi выполняется условие:
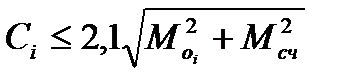 ,
,
то промахов в навигационной прокладке нет, и счислимые координаты места судно рекомендуется принять в совместную обработку с координатами обсервованными. Тогда вес счислимых координат Рcчi принимается обратным квадрату среднеквадратической погрешности счислимого места Мсч:
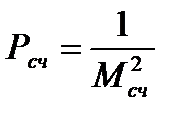 .
.
Основой аналитического метода отыскания координат вероятнейшего места судна является метод наименьших квадратов, сущность которого заключается в отыскании таких значений вероятнейших поправок к счислимым координатам Djв и Dlв, при которых сумма квадратов невязок для каждой из обсерваций являлась бы величиной минимальной.
Аналитическое решение сводится к вычислению координат вероятнейшего (осредненного) места jв и lв по формулам весового среднего:
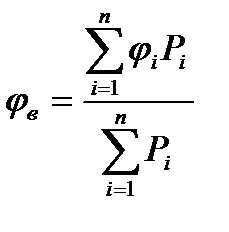 ;
;
 ;
;
где n – количество точек, принятых к осреднению;
ji, li - координаты точек, принятых к осреднению;
Рi - веса точек, принятых к осреднению.
Центрографический способ (рис. 9.1) более прост и удобен. Он заключается в следующем:
- вычисляются веса точек, принятых к осреднению;
- обсервованные точки попарно соединяется прямыми линиями. На каждом из отрезков находится точка, делящая его в отношении, обратно пропорциональном весам осредняемых точек. Этой такой точке приписывается вес, равный сумме весов двух осредняемых точек.
- полученные точки в свою очередь осредняются до теx пор, пока не будет найдена точка, вес которой равен сумме весов всех осредняемых точек. Эта точка и принимается за вероятнейшее место судна.
Рис. 9.1. Определение вероятнейшего места судна центрографическим способом
Среднеквадратическая погрешность полученного вероятнейшего места судна вычисляется формуле:
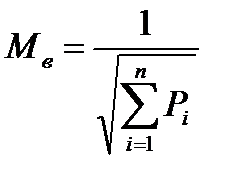 .
.
Требования ИМО к точности места судна, оборудованного приемной аппаратурой глобальной навигационной спутниковой системы, регламентируются Резолюцией ИМО А.953 от 05.12.2003 г. Минимальные общие требования данной Резолюции в зависимости от района плавания по обеспечению навигационной безопасности судовождения приведены в Приложении 1.
Детализация требований данной Резолюции применительно к конкретным районам и морским операциям приведены в Приложении 2.
10. Оценка точности счислимых координат места судна
Точность счисления пути судна зависит от точности учитываемых элементов счисления. Для расчета среднеквадратической погрешности счисления Мс(t) используется величина Кс - коэффициент счисления, зависящий от района плавания, степени изученности течений и точности их учета, от гидрометеорологических условий плавания, от типа судна, состава его технических средств навигации и точности учета элементов счисления.
Среднеквадратическая погрешность счисления изменяется:
- при интервалах счисления при t ≤ 2 часов по линейному закону:
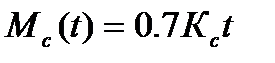 ;
;
- при интервалах счисления при t ≤ 2 часов по параболическому закону:
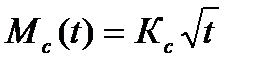 ,
,
где Mc(t) - cреднеквадратическая погрешность счисления в милях;
t - интервал счисления в часах;
Среднеквадратическая погрешность счислимого места судна рассчитывается с учетом точности исходной обсервации по формуле:
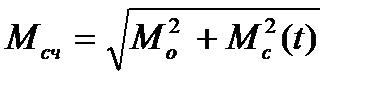 ;
;
где Мо - среднеквадратическая погрешность исходной обсервации.
Счислимо-обсервованным местом судна называется обсервованное место, полученной по результатам обработки двух навигационных параметров, измеренных в разные моменты времени. Особенностьюсчислимо-обсервованного места является то, что в погрешность определения координат, помимо погрешностей измерения и обработки навигационных параметров, входит и погрешность счисления, то есть при прочих равных условиях точность счислимо-обсервованного места всегда ниже точности обсервованного.
Примерами получения счислимо-обсервованного места судна являются такие способы определения координат, как способ крюс-пеленга и астрономический способ определения по разновременно измеренным высотам Солнца.
Радиальная среднеквадратическая погрешность счислимо-обсервованного места судна Мсо для неравноточных и взаимозависимых навигационных параметров рассчитывается по формуле:
 ,
,
где Θ - угол пересечения линий положения;
mЛП1 и mЛП2 - среднеквадратическиея погрешности линий положении;
Мс(t) - среднеквадратическая погрешность счисления.
Для неравноточных и независимых навигационных параметров данная формула выглядит как:
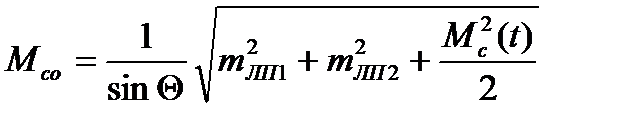 .
.
Величина коэффициента счисления Кс может быть рассчитана как априорно, так и апостериорно.
Для априорного (по известным статистическим погрешностям основных элементов счисления) расчета используется формула:
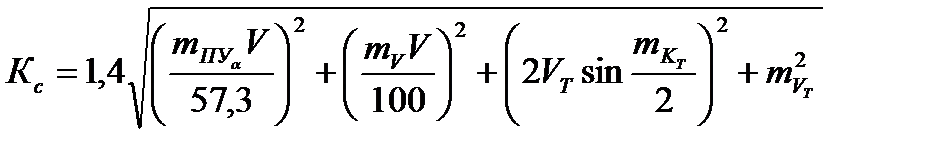 ,
,
где 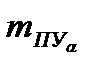 - погрешность определения угла дрейфа;
- погрешность определения угла дрейфа;
 - погрешность определения скорости судна;
- погрешность определения скорости судна;
 - погрешность определения курса течения;
- погрешность определения курса течения;
 - погрешность определения скорости течения;
- погрешность определения скорости течения;
V - скорость судна;
VТ - скорость течения.
Апостериорно (опытным путем - по совокупности невязок) величина коэффициента счисления Кс рассчитывается следующим образом:
а. Из всей совокупности невязок выбираются те, для которых t≤2 часов и для них рассчитывается значение коэффициента счисления Кс1 по формуле:
 ;
;
 ,
,
где n1 – общее количество невязок Сi для t≤2 часов;
б. Из всей совокупности невязок выбираются те, для которых t>2 часов и для них рассчитывается значение коэффициента счисления Кс2 по формуле:
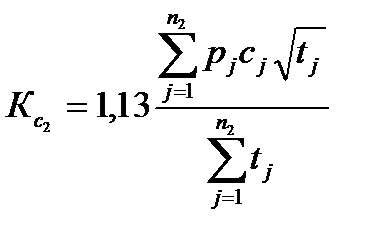 ;
;
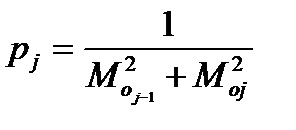 ,
,
где n2 – общее количество невязок Сj для t>2 часов;
в. Рассчитываются среднеквадратические погрешности mКс1 и mКс2 коэффициента счисления Кс1 и Кс2:
 ;
;
 ;
;  ;
;
 ;
;
г. Рассчитывается значение коэффициента счисления Кс для всей совокупности невязок по формуле:
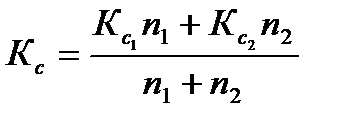 ,
,
д. Рассчитывается среднеквадратическая погрешность коэффициента точности счисления mКс всей совокупности невязок по формуле:
 ;
;
Если использовались равноточные измерения навигационных параметров, производимых через примерно равные интервалы времени, то:
 - t≤2 часов,
- t≤2 часов,
 - t>2 часов,
- t>2 часов,
Необходимое количество невязок n для определения коэффициента точности счисления Кс с его заданной среднеквадратической погрешностью mКс определяется по формуле:
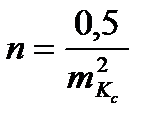 .
.
Для определения коэффициента точности счисления Кс со среднеквадратической погрешностью mКс не более 0,1 требуется обработать не менее 50 невязок.
Обсервационное счисление - это метод определения координат и элементов движения судна, основанный на комплексированном использовании информации, непрерывно поступающей от автономных судовых технических средств судовождения, и информации, получаемой в результате практически непрерывного измерения навигационных параметров относительно навигационных ориентиров.
B каждом цикле обсервационного счисления измеряется одна (или несколько) навигационная изолиния. Если измеряется одна изолиния, обработка информации производится в реальном масштабе времени. В противном случае производится накопление информации и приведение ее к одному моменту.
При приближенно линейном характере связи измеренных навигационных параметров с искомыми величинами математической основой обработки навигационной информации в процессе обсервационного счисления является оптимальный фильтр Калмана. При последовательном уточнении нескольких навигационных величии (например, двух координат и вектора скорости сноса) рекуррентная формула линейной оптимальной фильтрации имеет следующий вид
X=Xс+SHT(HSHT+R)-1(Z-Zс)
где X - вектор (матрица-столбец) искомых величин;
Xс - вектор (матрица-столбец) счислимых навигационных величин, найденных по результатам всего комплекса предыдущих измерений;
S - корреляционная матрица счислимых навигационных величин;
H - матрица коэффициентов исходных уравнений, связывающих измеренные и искомые навигационные величины;
HT- транспонированная матрица коэффициентов;
R - корреляционная матрица погрешностей измеренных навигационных величин;
Z- вектор (матрица-столбец) результатов измерения;
Zс- вектор (матрица-столбец) счислимых величин, соответствующих измеренным.
Точность полученного вектора X оценивается корреляционной матрицей:
P= SHT(HSHT+R)-1(HT)-1R
Если, например, при обсервационном счислении по каждому последовательно измеренному навигационному параметру определяются вероятнейшие координаты и элементы сноса, то матрицы рекуррентной формулы (без учета корреляции) имеют следующий вид:
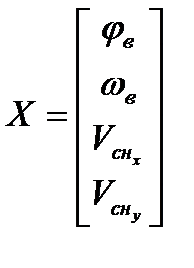 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ,
,
где φв, ωв - вероятнейшие широта и отшествие;
 ,
, 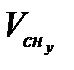 - составляющие вероятнейшего вектора сноса по меридиану и параллели;
- составляющие вероятнейшего вектора сноса по меридиану и параллели;
a, b - коэффициенты уравнения линии положения;
t - интервал счисления между двумя последовательными измерениями навигационного параметра;
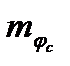 ,
,  - среднеквадратические погрешности счислимой широты и отшествия;
- среднеквадратические погрешности счислимой широты и отшествия;
 ,
,  - среднеквадратические погрешности составляющих скорости судна по меридиану и параллели;
- среднеквадратические погрешности составляющих скорости судна по меридиану и параллели;
 - среднеквадратическая погрешность скорости судна;
- среднеквадратическая погрешность скорости судна;
 ,
, 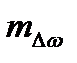 - среднеквадратические погрешности поправок широты и отшествия;
- среднеквадратические погрешности поправок широты и отшествия;
∆φc, ∆ωc - счислимые поправки, т. е. поправки к счислимой точке на линии истинного курса, рассчитанные по данным сноса, определенного в предыдущем цикле (по предшествующему навигационному параметру):
 ;
;
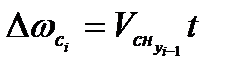 ;
;
∆φизм , ∆ωизм - измеренные поправки, равные:
∆φизм = ∆φс + ∆φо;
∆ωизм = ∆ωс + ∆ωо,
здесь ∆φо, ∆ωо - поправки для перехода от счислимого места судна к вероятнейшему месту, определенному по последней измеренной линии положения;
U и Uс - измеренный и счислимый навигационные параметры.
B данном случае измеренные навигационные параметры считаются корреляционно независимыми (корреляционные матрицы диагональные). Элементы сноса судна (направление и скорость) рассчитываются по формулам:
 ;
;
 .
.
Величина SHT(HSHT+R)-1 = K называется коэффициентом усиления. Этот коэффициент характеризует степень уточнения счислимых навигационных элементов по данным измеренных навигационных параметров.
Требования ИМО к точности места судна, оборудованного приемной аппаратурой глобальной навигационной спутниковой системы, регламентируются Резолюцией ИМО А.953 от 05.12.2003 г. Минимальные общие требования данной Резолюции в зависимости от района плавания по обеспечению навигационной безопасности судовождения приведены в Приложении 1.
Детализация требований данной Резолюции применительно к конкретным районам и морским операциям приведены в Приложении 2.
Приложение 1
Минимальные общие требования к глобальной навигационной спутниковой системе по обеспечению навигационной безопасности судовождения (Резолюция ИМО А.953 от 05.12.2003 г.)
| Технические требования | Плавание на входах в порты, подходах к портам и в прибрежных водах с высокой интенсивностью судоходства и (или) высоким уровнем риска | Плавание на входах в порты, подходах к портам и в прибрежных водах с низкой интенсивностью судоходства и(или) менее значительным уровнем риска | Плавание в океанских водах |
| Погрешность определения места судна с вероятностью 0.95 (м) | |||
| Рабочая зона | весь этап плавания | весь этап плавания | весь этап плавания |
| Обновление рассчитываемых и отображаемых обсервованных координат места судна не реже, чем: | один раз в 10 сек. | один раз в 10 сек. | один раз в 10 сек. |
| Обновление рассчитываемых и отображаемых обсервованных координат места судна при использовании АИС, графического представления местоположения или непосредственно для управления судном не реже, чем: | один раз в 2 сек. | один раз в 2 сек. | один раз в 2 сек. |
| Вероятность определения места судна для 2-х летнего периода | 0,995 | 0,995 | |
| Вероятность определения места судна для 30-дневного периода | 0,9997 | 0,9985 | 0,998 |
| Предупреждение о факте нерабочего состояния системы | <10 сек | <10 сек | <10 сек |
à - Для судов с эксплуатационной скоростью свыше 30 узлов могут быть более жесткие требования.
Приложение 2
Детализация минимальных требований к глобальной навигационной спутниковой системе по обеспечению навигационной безопасности судовождения.
(Дополнения 2,3 Резолюции ИМО А.953 от 05.12.2003 г.)
Поиск по сайту: