Сферический треугольник

Сферическим треугольником называется треугольник на сферической поверхности, который образован пересечением трех дуг больших кругов, например, двух меридианов и дуги большого круга (ортодромии, вертикала). Дуга большого круга проходит через известные две точки на поверхности Земли. Любой сферический треугольник содержит шесть элементов: три угла и три стороны. В общем случае углы в сферическом треугольнике (рис. 3.1.) принято обозначать большими буквами (например А,В,С), а противолежащие углам стороны соответствующими малыми буквами (например a, b, c). Любой сферический треугольник можно решить, если будут известны какие-либо три его элемента.

Для нахождения неизвестных элементов по трем известным (заданным) элементам сферического треугольника используются четыре основные формулы сферической тригонометрии.

Рис 3.1. Сферический треугольник.

Формула косинуса стороны. Во всяком сферическом треугольнике косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов этих же сторон на косинус угла между ними:

cos a = cos b cos c + sin b sin c cos A.

Формула косинуса угла. Во всяком сферическом треугольнике косинус угла равен отрицательному произведению косинусов двух других углов плюс произведение синусов этих же углов на косинус стороны между ними:

cos А = - cos B cos C + sin B sin C cos a.

Формула синусов. Во всяком сферическом треугольнике синусы сторон относятся как синусы противолежащих углов:

или .

Формула четырех рядом лежащих элементов (формула котангенсов). Во всяком сферическом треугольнике котангенс крайнего угла, умноженный на синус среднего угла, равен произведению котангенса крайней стороны на синус средней стороны минус произведение косинусов средних элементов:

ctg A sin B = ctg a sin c - cos c cos B;

или

ctg A = ctg a sin c cosec B - cos c ctg B.

Лучшим решением сферического треугольника является такое, при котором искомые элементы вычисляются по заданным элементам, без использования уже найденных.

Сферические треугольники решают с помощью таблиц тригонометрических функций и средств вычислительной техники

Ортодромией называется кратчайшее расстояние между двумя точками на поверхности сферы. Она измеряется по меньшей дуге большого круга, образованного пересечением плоскости проходящей через центр сферы и заданные точки, со сферической поверхностью.

Длина ортодромии S_ортвычисляется из сферического треугольника (рис.3.2) по формуле косинуса стороны:

сos S_орт= cos(90°- j₁) cos(90°- j₂) + sin(90°- j₁) sin(90°- j₂) cos(λ₂ – λ₁),

или:

сos S_орт= sin j₁ sin j₂ + cos j₁ cos j₂ cos Δλ

Направление ортодромии в точке T₁ (ОртП₁=А₁)определяется по формуле котангенсов:

ctg A₁ sin(λ₂ – λ₁) = ctg(90°- j₂) sin (90°-j₁) - cos(90°-j₁) cos (λ₂ – λ₁),

или:

ctgA₁=tg j₂ cos j₁ соsec Δλ - sin j₁ ctg Δλ.

Направление в точке Т₂(из точки Т₂в точку Т₁) определяется по формуле:

ctgA₂=tg j₁ cos j₂ соsec (λ₁ – λ₂) - sin j₂ ctg (λ₁ – λ₂).

Полученное направление ортодромии необходимо перевести в круговой счёт.

Рис. 3.2. Сферический треугольник на земной сфере для северной и для южной широты.

Локсодромией называется линия на поверхности Земли, которая пересекает все меридианы под одним и тем же углом.

Направление локсодромии, т. е. локсодромический курс К (пеленг) можно определить из уравнения (рис. 3.3):

;

где - ω – отшествие (плавание по параллели);

- ∆φ – разность широт;

- ∆λ – разность долгот.

Рис. 3.3. Вычисление длины локсодромии.

Если координаты пунктов отхода Т₁ и прихода Т₂ известны, то отшествие можно вычислить по формулам:

ω=Dλcosφ_ср;

φ_ср=(φ₁+ φ₂)/2.

Длину локсодромии S_локмежду двумя заданными точками Т₁и Т₂можно вычислить по одной из формул:

S_лок=∆φ secK;

S_лок= ωcosecK;

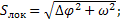
Для вычисления локсодромического курса на сфероиде используется формула:

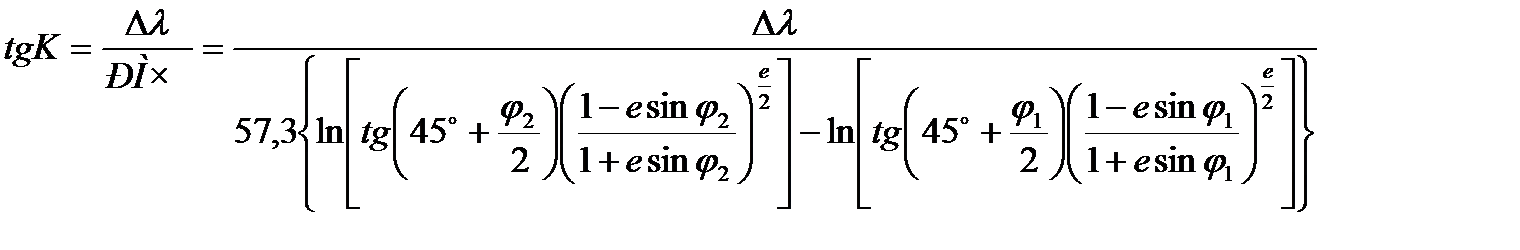
где - е – эксцентриситет земного сфероида (е = 0,081813324);

- РМЧ – разность меридиональных частей.

Разность меридиональных частей (значение в фигурных скобках) получается из таблицы 2.28а МТ-2000 или из таблицы 26 МТ-75 по известным φ₁ и φ₂.

На поверхности сфероида длина локсодромии вычисляется по формуле:

.

При вычислении длин ортодромии и локсодромии следует учитывать, что S_орт, S_лок, ∆φ и ω выражаются в морских милях, а Dλ и РМЧ - в экваториальных милях.

Схождением меридианов γназывается разность углов, под которыми ортодромия пересекает меридианы двух точек (рис. 3.4), т. е.

γ=А₂-А₁

Рис. 3.4. Схождение меридианов.

На сравнительно небольших расстояниях между точками Т₁и Т₂(500-600 миль) разности широт и долгот будут невелики. В этом случае величину схождения меридианов можно определить по формуле:

γ=Dλsinsφ_ср.

Если известно направление в точке Т₁то направление в точке Т₂можно получить по формуле:

А₂=А₁+γ.

Знак поправки γ определяется ∆ λи φ_ср.

Поиск по сайту: