Метод итераций. Уравнение f(x) необходимо представить в виде x = j (x)

Уравнение f(x) необходимо представить в виде x = j (x). Выберем теперь на участке [a, b] (участок, в котором находится корень уравнения) произвольную точку x₀ и последовательно будем вычислять:

x₁ =j (x₀), x₂ = j (x₁),..., x_k = j (x_k-1).

Обычно в качестве x₀ выбирают левую границу интервала [a, b].

Процесс последовательного вычисления значений x_k (k = 1, 2,...) по указанным формулам называется итерационным процессом (процессом последовательных приближений).

Задача. Решить уравнение ; отрезок, на котором существует корень, [2; 3].

Преобразуем уравнение .

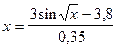Var x0, x1, eps: real;

begin

write (‘ введите начальное приближение’);

readln (x0);

write (‘введите абсолютную погрешность’);

readln (eps);

x1:= (3*sin(sqrt(x0)) - 3.8)/0.35;

while abs(x0 - x1) > eps do

begin

x0:= x1;

x1:= 3*sin(sqrt(x0) - 3.8)/0.35

end;

writeln (‘ решение уравнения х =’, x0)

end.

Поиск по сайту: